Table of Contents
- Introduction
- Desirable Algorithm Properties
- Existing Algorithms
- Ray casting
- Shadow casting (point-to-tile or point-to-point)
- Diamond walls (point-to-tile or point-to-point)
- Half-width walls (point-to-tile or point-to-point)
- Permissive field of view (tile-to-tile)
- Digital field of view (diamond-to-diamond)
- My algorithm
- Comparison
- Code
- Further Possibilities
Introduction
One task when implementing a roguelike is to figure out how to compute the region of the dungeon that's visible to the player or another monster. There are many existing algorithms, but they all have flaws, so I set out to develop a new algorithm that is fast, exact, and aesthetically pleasing to me. Although I didn't create a perfect algorithm, I still think my algorithm is an improvement over the others.
The visible region is called a monster's field of view, and determines whether the monster can see a particular part of the dungeon terrain. I'll assume that the dungeon is tile-based, which is usual. Whether the player can see a tile (called having line of sight and abbreviated LOS) is occasionally different from whether the player can see a monster in that tile, and frequently different from whether he can target that monster with a ranged weapon or spell (called having line of targeting here and abbreviated LOT).
Desirable Algorithm Properties
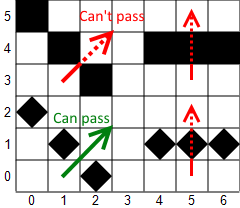
I'll first describe some frequently desirable traits of a field-of-view algorithm and then show why most existing algorithms lack one or more of these traits.- Symmetry: If you can see tile B while standing on tile A, then you should be able to see tile A when standing on tile B. This is generally considered desirable, partly because it's fair, and partly because the asymmetry in vision that almost all asymmetrical algorithms produce leads to poor tactical gameplay when the line of targeting is the same as the line of sight (as is normally the case). An algorithm that manages to be asymmetrical in the opposite of the normal way might actually be better than a symmetric algorithm.
- Expansive walls: When standing in a (convex) room, you can see all of the room's walls, and when standing in a long corridor you can see all the wall tiles along the sides of the corridor. Although it rarely affects gameplay tactics much, it looks ugly and can make exploration tedious if an algorithm does not have this property.
- Expanding pillar shadows: When sight is blocked by a pillar (an opaque tile not connected to others), the pillar should cast a shadow in the shape of a circular sector. This usually allows for more tactical gameplay, since it's easier to hide from, ambush, and escape other monsters. However, many roguelikes don't generate pillars, making this less relevant for them.
- No blind corners: You can see at least two tiles around a corner, so that if you move diagonally around the corner, you won't find yourself next to (and being gored by) a monster you couldn't see. This also implies that you can see at least two tiles to either side before stepping into a hallway. This is desirable in most cases, since it's tedious if players must step carefully around every corner. Some algorithms allow you to see infinitely far around corners, protecting you from monsters with ranged weapons as well.
- No artifacts: Although there can be reasonable disagreement over what the "right" behavior is for a field-of-view algorithm, an algorithm should at least do what it's supposed to. Generally this means that the algorithm should define the world geometry and accurately model light propagation within that geometry. The main causes of artifacts are the algorithm simply not corresponding to the world geometry, the algorithm being implemented using approximate rather than exact math, and bugs in the implementation.
- Efficiency: The algorithm shouldn't take a long time, and preferrably should avoid testing the same tiles repeatedly.
Existing Algorithms
This is not an exhaustive list of algorithms, but covers the most frequently used ones.
Ray casting
Pros: Simple. Pretty fast. Expanding pillar shadows. Good balance of light and shadow. No blind corners. Cons: Asymmetrical. Lots of gaps. No expansive walls. Quirky.Ray casting involves casting rays from the player to every point along the edge of the map or every point along the circumference of the player's view radius. The rays are cast using a simple line-drawing algorithm, usually Bresenham's, which stops as soon as it hits a wall. Ray casting is the simplest algorithm, and quite fast, but it has numerous problems. First, it's highly asymmetrical. Bresenham's algorithm isn't symmetrical, but even if you use a symmetrical line-drawing algorithm (which causes its own problems), the result will still be asymmetrical because the endpoints of the lines aren't simply reversed when you alternate positions. The algorithm also has gaps in both visible points and shadows and is generally very quirky. Gaps in the walls can be fixed up in a post-processing pass, which removes the ugliest artifacts, but this slows the algorithm and doesn't fix the other problems. The algorithm tests tiles multiple times, making it somewhat inefficient, but due to its simplicity it still ends up being pretty fast, especially with a small sight radius. (Ray casting has a reputation for being the fastest algorithm by far, but that's mainly due to people's generally poor implementations of more complex algorithms. A well-implemented shadow casting algorithm beats ray casting every time.) Leaving aside the numerous gaps and asymmetries and just considering the shapes of light and shadow, ray casting produces nicer results in my opinion than more complicated algorithms like shadow casting and diamond walls. Also, most of its problems become less severe as the sight radius decreases, and with a circular sight radius of 4 or less it actually works very nicely, with no post-processing required (although some artifacts remain).
───────────────────┤ ∙@∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ─────┬┬─∙┌┬──┐∙∙∙∙∙+ ├┘∙∙└┤ └─────┤
(can be fixed with post-processing)
∙∙∙∙∙∙∙∙∙∙∙∙ ∙@∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙┼∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙@∙∙∙∙∙∙ ∙∙∙∙┼∙┼∙┼∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙
───────────────── @∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┬┬─∙┌┬──┐∙∙∙ ├┘∙∙└┤ └───
───────────────── ∙@∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┬┬─∙┌┬──┐∙∙∙ ├┘∙∙└┤ └───
───────────────── ∙∙@∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┬┬─∙┌┬──┐∙∙∙ ├┘∙∙└┤ └───
Code to implement ray casting is below.
Shadow casting (point-to-tile or point-to-point)
Pros: Fast. Expanding pillar shadows. Expansive walls. Continuous point visibility. Cons: Diagonal vision much narrower than cardinal. Blind corners. Beam expands too much through a door. Asymmetrical. Nontrivial to eliminate all artifacts.Shadow casting is the technique of casting circular sectors of light outward from the player. When a sector hits a wall, the sector may be reduced in angle or split into two sectors which are then processed independently. Implementations vary, but a good implementation will visit each tile only once, or nearly so, and a small and roughly constant amount of work is done per tile. This makes shadow casting one of the fastest algorithms if implemented well, but in poor implementations it can perform relatively slowly in diagonal tunnels and in open areas with lots of small obstructions. "Shadow casting" is a bit of a misnomer because what's actually cast is light, but I'll use it since "light casting" seems too similar to "ray casting". In every case I've seen, shadow casting has used square tiles, but other tile shapes are possible.
In the usual implementation, shadow casting renders a tile visible if there is an unobstructed line from the center of the player's tile to any part of the target tile. Here's an example to illustrate how shadow casting works for a single octant. (Not all implementations work in octants.) In the first picture, a 45-degree sector of light is projected down the 45-degree octant. The green line bounds the top of the sector and the blue line bounds the bottom. The fractions displayed are the slopes of the lines, which are always from 0 to 1 (inclusive). Tiles with circles are considered visible. Then, the algorithm works from left to right (increasing X). For each column, it scans from the top tile within the sector down to the bottom tile within the sector. If a transition from clear to opaque or vice versa is found, the sector is adjusted. In the second picture, the first three columns have been scanned and a transition from opaque to clear has been found in the fourth column, so the top vector is adjusted downward. In the next picture, a clear-to-opaque transition has been found and the bottom vector is adjusted upward. In the final picture, you can see that both types of transitions were found in the fifth column, so the sector splits into two sectors, each of which continue independently. The algorithm stops when it hits the maximum sight distance or all the sectors become empty (bottom slope > top slope).
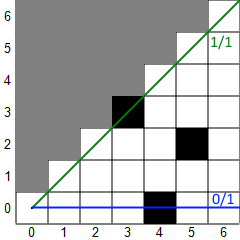
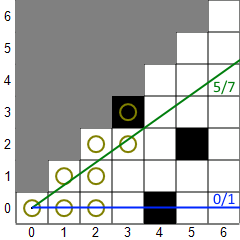
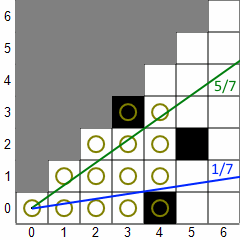
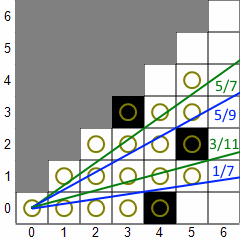
Here are some of the features and problems of shadow casting (with the usual square tiles).
∙∙∙@┼∙∙∙∙∙ ∙∙∙┼∙∙∙∙∙∙ ∙∙┼∙∙∙∙∙∙∙ ∙┼∙∙∙∙∙∙∙∙ ┼∙∙∙∙∙∙∙∙∙
∙∙∙@┼∙∙∙┼∙ ∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙┼∙∙∙┼∙ ∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙
─────────── ∙∙∙∙∙∙∙∙∙∙∙ ──┬┬─@┌┬─── ├┘∙∙└┤ ┌┘∙∙│∙└┐
─────────── @∙∙∙∙∙∙∙∙∙∙ ─────┬┬─∙┌┬ ├┘∙∙└┤ ┌┘∙∙│∙└
(compare w/ previous)
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙┼∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
(not an artifact, just ugly)
∙∙∙∙∙∙∙∙∙│ ∙∙∙∙┼∙│∙∙│ ∙∙∙∙∙∙│∙∙│ ∙∙∙∙∙∙∙∙∙└─ ∙@∙∙∙│∙∙∙∙∙
(implementation artifact)
∙│ │∙∙∙∙∙∙∙∙∙∙∙ ∙└───────────────────┤∙∙∙∙∙∙∙┼∙∙∙ @∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙ ───────┬┬─∙┌┬────────┤∙∙∙∙∙∙∙┼∙∙∙ ├┘∙∙└┤ │∙∙∙∙∙∙∙∙∙∙∙
(not an artifact, but very ugly)
The asymmetry displayed above is an example of how asymmetrical algorithms tend to create unsatisfying tactical situations. If you can target what you can see, then the monster in the middle of the corridor would have an advantage over a monster on the side of it, despite the monster on the side appearing to have better cover. The monster on the side could be shot without even seeing the attacker. Asymmetries like these are why symmetry is considered a desirable property. However, if the asymmetry was reversed, it might actually be an improvement over symmetrical algorithms by allowing you to take cover, giving a more tactical feel to the gameplay (although it would probably be best if the visibility was symmetrical but not the targeting). There is an algorithm called "reverse shadow casting" which reverses the asymmetry, but it generally looks much poorer and runs much slower.
A small modification to the shadow casting code suffices to make it symmetrical, though. This works by changing the algorithm so it considers a tile visible only if there's an unobstructed line from the center of the player's tile to the center of the target tile (rather than any part of the target tile). This fixes some problems and causes others, as you can see below.
─────────── @∙∙∙∙∙∙∙∙∙∙ ─────┬┬─∙┌┬ ├┘∙∙└┤ ┌┘∙∙│∙└
no expansive walls
┌────── │∙∙∙∙∙∙ │∙∙∙∙∙∙ │∙∙∙∙∙∙ │@∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙┼∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙│ ∙∙∙∙┼∙│∙∙│ ∙∙∙∙∙∙│∙∙│ ∙∙∙∙∙∙∙∙∙└─ ∙@∙∙∙│∙∙∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
Code to implement basic shadow casting is below.
Diamond walls (point-to-tile or point-to-point)
Pros: Pretty fast. Expanding pillar shadows. Expansive walls. No blind corners. Mostly continuous point visibility. Cons: Beam expands too much through a door. Asymmetrical; a small change fixes this but loses expansive walls and causes more visual discontinuities.Like shadow casting, the diamond walls algorithm treats a tile as visible if there's an unobstructed line from the center of the player's tile to any part of the target tile. However, for the purpose of occlusion it treats walls as though they were diamonds (embedded in the tile, the remainder being empty space). This eliminates the thin diagonal spaces from the standard shadow casting algorithm and allows better peeking around corners, but it causes a couple problems of its own. The main new problem is that it is, in my opinion, a bit too permissive, meaning that it makes too many tiles visible. Nonetheless it seems like an improvement on standard shadow casting. (I chose to implement it by modifying my shadow casting code.) As for efficiency, it is somewhat slower than plain shadow casting, since it needs to do more work per tile, but it's still reasonably fast.
Treating walls as diamonds actually makes a lot of sense in roguelikes, although it sounds ridiculous. The reason is that most roguelikes allow monsters to move between diagonally adjacent walls, and if the walls were square, their corners would be touching, leaving no space. This is illustrated in the picture below. Making the physics of the world more consistent naturally leads to more intuitive lighting. Diamond walls also allow better vision around corners, which is usually desirable.
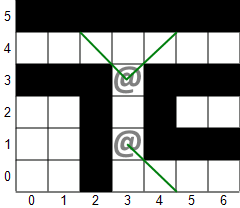
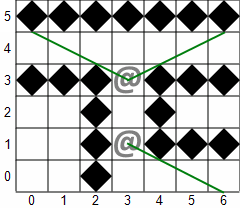
Unfortunately, there is a theoretical problem with diamond walls. The description states that lines tangent to a wall diamond aren't considered to intersect it and zero-width beams of light still illuminate tiles. This provides better vision around corners but also allows the following case where a monster can see through a wall. Implementations are expected to disallow seeing through walls as a special case, which prevents the problem but requires inconsistent physics.
Here are some features and problems of shadow casting with diamond walls.
│∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙┼ ∙∙∙■∙∙∙∙∙┼@
@┼∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙┼∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙┼∙∙∙∙∙∙∙∙∙
─────────── ∙∙∙∙∙∙∙∙∙∙∙ ──┬┬─@┌┬─── ├┘∙∙└┤ ┌┘∙∙│∙└┐
─────────── @∙∙∙∙∙∙∙∙∙∙ ─────┬┬─∙┌┬ ├┘∙∙└┤ ┌┘∙∙│∙└
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙┼∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
than shadow casting
│∙∙∙∙∙∙∙∙∙∙∙ ───────────┤∙∙∙∙∙∙∙┼∙∙∙ @∙∙∙∙∙∙∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙ ∙┌┬────────┤∙∙∙∙∙∙∙┼∙∙∙ ∙└┤ │∙∙∙∙∙∙∙∙∙∙∙
The same simple change can be made to turn the diamond wall algorithm into a symmetric one, and it has the same benefits and drawbacks that it has for regular shadow casting.
─────────── @∙∙∙∙∙∙∙∙∙∙ ─────┬┬─∙┌┬ ├┘∙∙└┤ ┌┘∙∙│∙└
no expansive walls
──────────┐ ∙∙∙∙∙∙∙∙∙∙│ @∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙│
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙┼∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
├───∙────── │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙┼∙┼∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙│∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
Code to implement diamond walls is below.
Half-width walls
Pros & cons: The same as diamond walls, but more permissive and slightly slower.There is another idea similar to diamond walls except that it uses walls that are half the usual width. It also solves the problem of not being able to see between diagonal tiles, but in my opinion looks poorer than diamond walls by being too permissive. The implementation is also slightly slower since not every wall tile has the same shape. (The shape depends on whether there is an adjacent wall for it to join with.) I implemented the algorithm but I don't consider it worth the effort to present.
Permissive field of view (tile-to-tile)
Pros: Symmetry. No blind corners. Expansive walls. Continuous point visibility. Cons: Slow. No expanding pillar shadows. Perhaps too much visibility around corners.The permissive field of view algorithm treats a tile as visible if there's an unobstructed line from any part of the player's tile to any part of the target tile. Most implementations of this use an approximation, such as just testing the corners against each other, which fails in some cases. Exact implementations work in all cases but tend to be fairly slow. I provide an exact implementation (cleaned up and adapted from a demo by Jonathon Duerig). The main features of the algorithm are that it's symmetrical and allows peeking very far around corners, but it's too permissive for my taste, so I haven't made any effort to optimize the algorithm. That said, the algorithm looks and works much better if all creatures have a short sight radius.
There exists a version of the permissive FOV algorithm that allows the permissivity to be changed at runtime. I played with it, and half the usual permissivity looks decent to my eye, but then it's no longer symmetrical and I'd prefer to have a faster algorithm anyway.
│∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙ ∙∙∙■∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼@ │∙∙∙∙∙∙∙∙∙
@∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙┼∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
─┴─────────■─── ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ @┌─────────■─── ∙│∙∙∙∙∙∙∙∙∙∙∙∙∙ +┤∙∙∙∙∙∙∙∙│∙∙∙∙
│∙│ ┌┬───┐ │∙├┬────────────────┴┘∙∙∙│ │∙└┘∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙┌─┘ │@∙∙∙┌─────────────────┘ └────┘
Code to implement the permissive field of view algorithm is below.
Digital field of view (diamond-to-diamond)
Pros & cons: Same as the permissive field of view algorithm.The digital field of view algorithm treats every tile as a diamond (embedded in the square, the remainder being empty space) and considers a tile visible if there is an unobstructed line from any part of the player's diamond to any part of the target diamond. As a result, it's slightly more permissive than even the permissive field of view algorithm (since walls present less of an obstruction), but otherwise it shares all the same features and drawbacks while being even slower. The idea is based on the rather unwieldy concept of digital straight line segments, and I did not bother to create an implementation of it. One interesting feature of the algorithm is that the knowledge of the digital line segment from a line-of-sight calculation allows easy tracing of a projectile path through space without hitting any walls, even down somewhat twisted tunnels (such as the Kuo corridor above). But the complexity seems to outweight the benefit.
My algorithm
None of the above algorithms really satisfy me. First of all, except for ray casting they're all either too permissive or too restrictive – sometimes both at once, and ray casting has too many artifacts to be usable. Here are the problems I intend to fix and the features I intend to have.- Less permissive than most other algorithms
- More symmetrical than other algorithms
- Able to be made symmetrical (at least versus non-passwall monsters) without losing expansive walls
- Good vision through diagonal spaces, but not too much
- Good light casting through narrow spaces, without losing expansive walls
- Reduced shadow gaps compared to other algorithms
- Efficiency on par with diamond walls
- No blind corners
- No artifacts
- Consistent physics
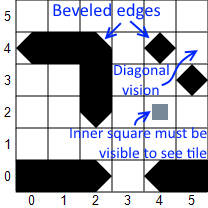
A corner is beveled if neither of the two cardinally adjacent tiles are walls. Wall tiles are considered visible if a beam of light intersects the wall shape while clear tiles are considered visible if light intersects the central square (which can be at most 1/2 the width or height of the tile). Tangents to a shape do not intersect it, and a zero-width sector of light can't illuminate anything.
Solid walls with beveled edges allow peeking around corners and seeing through diagonal spaces while avoiding the theoretical problem of diamond walls. Not showing clear tiles unless light passes near the center should make it a bit less permissive, reduce shadow gaps, reduce asymmetry, and fix the behavior of light passing through narrow spaces.
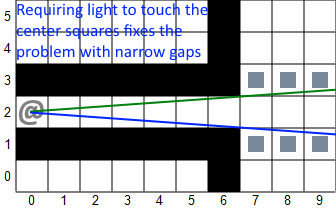
The problem with light passage through narrow spaces is illustrated in the second image above. No matter how far you are down the tunnel, the circular sector will open up as it leaves the narrow space and, with other algorithms, immediately illuminate the tiles above and below. As seen in the screenshots above, pillars cannot stop this illumination. The reason is that, like the walls of the tunnel, the sector is still opening up after it passes between the pillars. Not illuminating tiles only barely touched by light avoids this, and allows pillars to effectively stop the light. This should also reduce shadow gaps by preventing small slivers of light from dispelling the shadow from a tile.
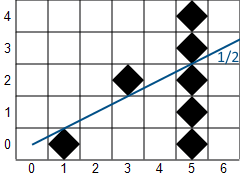
Permissivity can be tuned by adjusting the angle of the bevel and the size of the inner square. Another shape besides a square can be used, but it must fit within the area of the largest diamond that can be placed in the tile (i.e. it may not extend beyond the shape of a pillar). For a square, the maximum is 1/2 the width of the tile. Testing shows that using 1/2 the width gives good results. Using 3/8 the width of the tile allows for symmetrical sight between creatures in and on the side of a narrow corridor, which is a nice feature, but it looks a bit too restrictive otherwise (especially if there are many pillars), so I'll stick with 1/2. The actual implementation will use a modified shadow casting algorithm, giving decent performance as long as I can avoid doing too much work per tile.
Here are some samples from the asymmetrical version.
∙∙∙@┼∙∙∙∙∙ ∙∙∙┼∙∙∙∙∙∙ ∙∙┼∙∙∙∙∙∙∙ ∙┼∙∙∙∙∙∙∙∙ ┼∙∙∙∙∙∙∙∙∙
@┼∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙ ∙┼∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙ ∙┼∙∙∙∙∙∙∙∙
─────────── ∙∙∙∙∙∙∙∙∙∙∙ ──┬┬─@┌┬─── ├┘∙∙└┤ ┌┘∙∙│∙└┐
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙┼∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────────┤∙∙∙∙∙∙∙┼∙∙∙┼∙ @∙∙∙∙∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙ ┬────────┤∙∙∙∙∙∙∙┼∙∙∙┼∙ ┤ │∙∙∙∙∙∙∙∙∙∙∙∙∙
My algorithm has two symmetrical versions: one that's fully symmetrical and another that's symmetrical except for some walls (i.e. symmetrical between monsters except sometimes against passwall monsters). Here's the version that's mostly symmetrical. As you can see, it doesn't suffer from the same problems of other algorithms when made symmetrical. Most importantly, it doesn't lose the expansive walls feature. This is the better of the two symmetrical versions, unless you need symmetry versus passwall monsters.
─────────── @∙∙∙∙∙∙∙∙∙∙ ┬┬─∙┌┬───── ├┘∙∙└┤
expansive walls
──────────┐ ∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙│ @∙∙∙∙∙∙∙∙∙│
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙┼∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
Here is the fully symmetrical version of my algorithm. It gains symmetry against all passwall monsters but loses expansive walls as usual, although walls are no less expansive than other algorithms (except permissive FOV) and more expansive than most. It is very similar but not identical to symmetrical diamond walls.
─────────── @∙∙∙∙∙∙∙∙∙∙ ┬┬─∙┌┬───── ├┘∙∙└┤
no expansive walls
──────────┐ ∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙│ @∙∙∙∙∙∙∙∙∙│
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙┼∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
Code to implement my algorithm is below.
Comparison
Here's a comparison of my algorithm with the ray casting, shadow casting, diamond walls, and permissive field of view algorithms. Unless otherwise stated, the comparison is done between the basic (usually asymmetrical) versions of the algorithms. In some sections I've reduced the line height in order to make the height of a tile closer to its width, allowing a better sense of symmetry on the two axes. Depending on your font and browser, this might look terrible, especially in vertical walls. To toggle this effect, click here. (This requires Javascript, and the effect is only enabled initially if Javascript is available.)Corner peeking
─────────── ∙∙∙∙∙∙∙∙∙∙∙ ──┬┬─@┌┬─── ├┘∙∙└┤ ┌┘∙∙│∙└┐
─────────── ∙∙∙∙∙∙∙∙∙∙∙ ──┬┬─@┌┬─── ├┘∙∙└┤ ┌┘∙∙│∙└┐
─────────── ∙∙∙∙∙∙∙∙∙∙∙ ──┬┬─@┌┬─── ├┘∙∙└┤ ┌┘∙∙│∙└┐
─────────── ∙∙∙∙∙∙∙∙∙∙∙ ──┬┬─@┌┬─── ├┘∙∙└┤ ┌┘∙∙│∙└┐
─────────── ∙∙∙∙∙∙∙∙∙∙∙ ──┬┬─@┌┬─── ├┘∙∙└┤ ┌┘∙∙│∙└┐
Corridor asymmetry
Red tiles are where a monster can see the player but the player can't see the monster.
∙└─────────────────── ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───────┬┬─@┌┬──────── ├┘∙∙└┤ ┌┘∙∙│∙└┐
∙└─────────────────── ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───────┬┬─@┌┬──────── ├┘∙∙└┤ ┌┘∙∙│∙└┐
∙└─────────────────── ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───────┬┬─@┌┬──────── ├┘∙∙└┤ ┌┘∙∙│∙└┐
∙└─────────────────── ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───────┬┬─@┌┬──────── ├┘∙∙└┤ ┌┘∙∙│∙└┐
∙└─────────────────── ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───────┬┬─@┌┬──────── ├┘∙∙└┤ ┌┘∙∙│∙└┐
∙└─────────────────── ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───────┬┬─@┌┬──────── ├┘∙∙└┤ ┌┘∙∙│∙└┐
Narrow spaces
In this and subsequent sections I've reduced the line height of some sections in order to make the height of a tile closer to its width, allowing a better sense of symmetry on the two axes. Depending on your font and browser, this might look terrible, especially in vertical walls. To toggle this effect, click here. (This requires Javascript, and the effect is only enabled initially if Javascript is available.)
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙+∙∙∙+∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙+∙∙∙+∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙+∙∙∙+∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙+∙∙∙+∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙+∙∙∙+∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙+∙∙∙+∙ @∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙+∙∙∙+∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙+∙∙∙+∙ @∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙+∙∙∙+∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙+∙∙∙+∙ @∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙+∙∙∙+∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙+∙∙∙+∙ @∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙+∙∙∙+∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙+∙∙∙+∙ @∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙+∙∙∙+∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙
Diagonal spaces
∙∙∙∙∙∙∙+ ∙∙∙∙∙∙+∙ ∙∙∙∙∙+∙∙ ∙∙∙∙+∙∙∙ ∙∙∙+∙∙∙∙ ∙∙+∙∙∙∙∙ @+∙∙∙∙∙∙
∙∙∙∙∙∙∙+ ∙∙∙∙∙∙+∙ ∙∙∙∙∙+∙∙ ∙∙∙∙+∙∙∙ ∙∙∙+∙∙∙∙ ∙∙+∙∙∙∙∙ @+∙∙∙∙∙∙
∙∙∙∙∙∙∙+ ∙∙∙∙∙∙+∙ ∙∙∙∙∙+∙∙ ∙∙∙∙+∙∙∙ ∙∙∙+∙∙∙∙ ∙∙+∙∙∙∙∙ @+∙∙∙∙∙∙
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ ┤∙∙∙∙∙∙+ ■∙∙∙∙∙+@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ ┤∙∙∙∙∙∙+ ■∙∙∙∙∙+@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ ┤∙∙∙∙∙∙+ ■∙∙∙∙∙+@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ ┤∙∙∙∙∙∙+ ■∙∙∙∙∙+@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ ┤∙∙∙∙∙∙+ ■∙∙∙∙∙+@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙+ ┤∙∙∙∙∙+∙ ■∙∙∙∙+∙@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙+ ┤∙∙∙∙∙+∙ ■∙∙∙∙+∙@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙+ ┤∙∙∙∙∙+∙ ■∙∙∙∙+∙@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙+ ┤∙∙∙∙∙+∙ ■∙∙∙∙+∙@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙+ ┤∙∙∙∙∙+∙ ■∙∙∙∙+∙@
┌──────── │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙+ │∙∙∙∙∙∙+∙ │∙∙∙∙∙+∙∙ │∙∙∙∙+∙∙@
┌──────── │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙+ │∙∙∙∙∙∙+∙ │∙∙∙∙∙+∙∙ │∙∙∙∙+∙∙@
┌──────── │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙+ │∙∙∙∙∙∙+∙ │∙∙∙∙∙+∙∙ │∙∙∙∙+∙∙@
┌──────── │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙+ │∙∙∙∙∙∙+∙ │∙∙∙∙∙+∙∙ │∙∙∙∙+∙∙@
┌──────── │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙+ │∙∙∙∙∙∙+∙ │∙∙∙∙∙+∙∙ │∙∙∙∙+∙∙@
Rooms
┌───────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ┌┘∙──┬─────┐∙│ ┤∙∙∙∙│ │∙│ ┘∙∙∙∙│ │∙│ @∙∙∙∙└───┐ │∙│ ┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙∙│ │∙∙∙∙│ └─────┘
┌───────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ┌┘∙──┬─────┐∙│ ┤∙∙∙∙│ │∙│ ┘∙∙∙∙│ │∙│ @∙∙∙∙└───┐ │∙│ ┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙∙│ │∙∙∙∙│ └─────┘
┌───────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ┌┘∙──┬─────┐∙│ ┤∙∙∙∙│ │∙│ ┘∙∙∙∙│ │∙│ @∙∙∙∙└───┐ │∙│ ┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙∙│ │∙∙∙∙│ └─────┘
┌───────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ┌┘∙──┬─────┐∙│ ┤∙∙∙∙│ │∙│ ┘∙∙∙∙│ │∙│ @∙∙∙∙└───┐ │∙│ ┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙∙│ │∙∙∙∙│ └─────┘
┌───────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ┌┘∙──┬─────┐∙│ ┤∙∙∙∙│ │∙│ ┘∙∙∙∙│ │∙│ @∙∙∙∙└───┐ │∙│ ┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙∙│ │∙∙∙∙│ └─────┘
│ ┌───────────┐ │ │∙∙∙∙∙∙∙∙∙∙∙│ │ ┌┘∙──┬─────┐∙│ └─┬┤∙∙∙∙│ │∙│ ∙∙└┘∙∙∙∙│ │∙│ ┐∙∙∙∙∙∙∙└───┐ │∙│ └──┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙@│ │∙∙∙∙│ └─────┘
│ ┌───────────┐ │ │∙∙∙∙∙∙∙∙∙∙∙│ │ ┌┘∙──┬─────┐∙│ └─┬┤∙∙∙∙│ │∙│ ∙∙└┘∙∙∙∙│ │∙│ ┐∙∙∙∙∙∙∙└───┐ │∙│ └──┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙@│ │∙∙∙∙│ └─────┘
│ ┌───────────┐ │ │∙∙∙∙∙∙∙∙∙∙∙│ │ ┌┘∙──┬─────┐∙│ └─┬┤∙∙∙∙│ │∙│ ∙∙└┘∙∙∙∙│ │∙│ ┐∙∙∙∙∙∙∙└───┐ │∙│ └──┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙@│ │∙∙∙∙│ └─────┘
│ ┌───────────┐ │ │∙∙∙∙∙∙∙∙∙∙∙│ │ ┌┘∙──┬─────┐∙│ └─┬┤∙∙∙∙│ │∙│ ∙∙└┘∙∙∙∙│ │∙│ ┐∙∙∙∙∙∙∙└───┐ │∙│ └──┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙@│ │∙∙∙∙│ └─────┘
│ ┌───────────┐ │ │∙∙∙∙∙∙∙∙∙∙∙│ │ ┌┘∙──┬─────┐∙│ └─┬┤∙∙∙∙│ │∙│ ∙∙└┘∙∙∙∙│ │∙│ ┐∙∙∙∙∙∙∙└───┐ │∙│ └──┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙@│ │∙∙∙∙│ └─────┘
────────┬ ∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙│ ∙∙∙+∙│∙∙│ ∙∙∙∙∙│∙∙│ ∙∙∙∙∙∙∙∙└ @∙∙∙│∙∙∙∙
────────┬ ∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙│ ∙∙∙+∙│∙∙│ ∙∙∙∙∙│∙∙│ ∙∙∙∙∙∙∙∙└ @∙∙∙│∙∙∙∙
────────┬ ∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙│ ∙∙∙+∙│∙∙│ ∙∙∙∙∙│∙∙│ ∙∙∙∙∙∙∙∙└ @∙∙∙│∙∙∙∙
────────┬ ∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙│ ∙∙∙+∙│∙∙│ ∙∙∙∙∙│∙∙│ ∙∙∙∙∙∙∙∙└ @∙∙∙│∙∙∙∙
────────┬ ∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙│ ∙∙∙+∙│∙∙│ ∙∙∙∙∙│∙∙│ ∙∙∙∙∙∙∙∙└ @∙∙∙│∙∙∙∙
─────┬ ∙∙∙∙∙│ ∙∙∙∙∙│ +∙│∙∙│ ∙∙│∙∙│ ∙∙∙∙∙└ @│∙∙∙∙
─────┬ ∙∙∙∙∙│ ∙∙∙∙∙│ +∙│∙∙│ ∙∙│∙∙│ ∙∙∙∙∙└ @│∙∙∙∙
─────┬ ∙∙∙∙∙│ ∙∙∙∙∙│ +∙│∙∙│ ∙∙│∙∙│ ∙∙∙∙∙└ @│∙∙∙∙
─────┬ ∙∙∙∙∙│ ∙∙∙∙∙│ +∙│∙∙│ ∙∙│∙∙│ ∙∙∙∙∙└ @│∙∙∙∙
─────┬ ∙∙∙∙∙│ ∙∙∙∙∙│ +∙│∙∙│ ∙∙│∙∙│ ∙∙∙∙∙└ @│∙∙∙∙
┌─┐ │@└──┐ │∙∙∙∙│ └──┐∙│ │∙│ │∙└
┌─┐ │@└──┐ │∙∙∙∙│ └──┐∙│ │∙│ │∙└
┌─┐ │@└──┐ │∙∙∙∙│ └──┐∙│ │∙│ │∙└
┌─┐ │@└──┐ │∙∙∙∙│ └──┐∙│ │∙│ │∙└
┌─┐ │@└──┐ │∙∙∙∙│ └──┐∙│ │∙│ │∙└
┌─┘∙└┬─┐ │∙∙∙∙│∙│ │∙∙+∙∙∙│ │∙@∙∙∙∙│ └─┬+┬──┘
┌─┘∙└┬─┐ │∙∙∙∙│∙│ │∙∙+∙∙∙│ │∙@∙∙∙∙│ └─┬+┬──┘
┌─┘∙└┬─┐ │∙∙∙∙│∙│ │∙∙+∙∙∙│ │∙@∙∙∙∙│ └─┬+┬──┘
┌─┘∙└┬─┐ │∙∙∙∙│∙│ │∙∙+∙∙∙│ │∙@∙∙∙∙│ └─┬+┬──┘
┌─┘∙└┬─┐ │∙∙∙∙│∙│ │∙∙+∙∙∙│ │∙@∙∙∙∙│ └─┬+┬──┘
┌─┘∙└┬─┐ │∙∙∙∙│@│ │∙∙+∙∙∙│ │∙∙∙∙∙∙│ └─┬+┬──┘
┌─┘∙└┬─┐ │∙∙∙∙│@│ │∙∙+∙∙∙│ │∙∙∙∙∙∙│ └─┬+┬──┘
┌─┘∙└┬─┐ │∙∙∙∙│@│ │∙∙+∙∙∙│ │∙∙∙∙∙∙│ └─┬+┬──┘
┌─┘∙└┬─┐ │∙∙∙∙│@│ │∙∙+∙∙∙│ │∙∙∙∙∙∙│ └─┬+┬──┘
┌─┘∙└┬─┐ │∙∙∙∙│@│ │∙∙+∙∙∙│ │∙∙∙∙∙∙│ └─┬+┬──┘
│@└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙+∙+∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│∙┌┤ └────────┴─┴┘
│@└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙+∙+∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│∙┌┤ └────────┴─┴┘
│@└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙+∙+∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│∙┌┤ └────────┴─┴┘
│@└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙+∙+∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│∙┌┤ └────────┴─┴┘
│@└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙+∙+∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│∙┌┤ └────────┴─┴┘
│∙│ │∙└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙+∙+∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│@┌┤ └────────┴─┴┘
│∙│ │∙└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙+∙+∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│@┌┤ └────────┴─┴┘
│∙│ │∙└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙+∙+∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│@┌┤ └────────┴─┴┘
│∙│ │∙└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙+∙+∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│@┌┤ └────────┴─┴┘
│∙│ │∙└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙+∙+∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│@┌┤ └────────┴─┴┘
──────── ∙∙∙∙∙∙∙∙ ┬─∙┌┬─── ┘∙∙└┤ ∙∙│∙└┐ ∙┌┴┐∙└┐ ┌┘ └┐∙└┐ ┘ └┐@│
──────── ∙∙∙∙∙∙∙∙ ┬─∙┌┬─── ┘∙∙└┤ ∙∙│∙└┐ ∙┌┴┐∙└┐ ┌┘ └┐∙└┐ ┘ └┐@│
──────── ∙∙∙∙∙∙∙∙ ┬─∙┌┬─── ┘∙∙└┤ ∙∙│∙└┐ ∙┌┴┐∙└┐ ┌┘ └┐∙└┐ ┘ └┐@│
──────── ∙∙∙∙∙∙∙∙ ┬─∙┌┬─── ┘∙∙└┤ ∙∙│∙└┐ ∙┌┴┐∙└┐ ┌┘ └┐∙└┐ ┘ └┐@│
──────── ∙∙∙∙∙∙∙∙ ┬─∙┌┬─── ┘∙∙└┤ ∙∙│∙└┐ ∙┌┴┐∙└┐ ┌┘ └┐∙└┐ ┘ └┐@│
Pillars
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ @+∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ @+∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ @+∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ @+∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ @+∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙
┌────────── │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙┼∙ │∙∙∙∙∙∙∙∙∙@
┌────────── │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙┼∙ │∙∙∙∙∙∙∙∙∙@
┌────────── │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙┼∙ │∙∙∙∙∙∙∙∙∙@
┌────────── │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙┼∙ │∙∙∙∙∙∙∙∙∙@
┌────────── │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙┼∙ │∙∙∙∙∙∙∙∙∙@
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙+∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙+∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙+∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙+∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙+∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙+∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙+∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙+∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙+∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙+∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ @∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙
┌───────────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ ┤∙∙∙∙∙∙∙+∙@∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ │∙∙∙∙∙∙∙+∙∙∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┴───────────────────┴
┌───────────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ ┤∙∙∙∙∙∙∙+∙@∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ │∙∙∙∙∙∙∙+∙∙∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┴───────────────────┴
┌───────────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ ┤∙∙∙∙∙∙∙+∙@∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ │∙∙∙∙∙∙∙+∙∙∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┴───────────────────┴
┌───────────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ ┤∙∙∙∙∙∙∙+∙@∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ │∙∙∙∙∙∙∙+∙∙∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┴───────────────────┴
┌───────────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┤∙∙∙∙∙∙∙+∙∙∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ ┤∙∙∙∙∙∙∙+∙@∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ │∙∙∙∙∙∙∙+∙∙∙+∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┴───────────────────┴
──────────────┐ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙├ @∙∙∙∙∙∙∙∙∙∙∙∙∙+ ∙∙+∙∙∙∙∙∙∙∙∙∙∙├ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ──────────────┤
──────────────┐ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙├ @∙∙∙∙∙∙∙∙∙∙∙∙∙+ ∙∙+∙∙∙∙∙∙∙∙∙∙∙├ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ──────────────┤
──────────────┐ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙├ @∙∙∙∙∙∙∙∙∙∙∙∙∙+ ∙∙+∙∙∙∙∙∙∙∙∙∙∙├ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ──────────────┤
──────────────┐ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙├ @∙∙∙∙∙∙∙∙∙∙∙∙∙+ ∙∙+∙∙∙∙∙∙∙∙∙∙∙├ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ──────────────┤
──────────────┐ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙├ @∙∙∙∙∙∙∙∙∙∙∙∙∙+ ∙∙+∙∙∙∙∙∙∙∙∙∙∙├ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ──────────────┤
+∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙+∙+∙+∙+∙∙ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ +∙+∙+∙+∙+∙+ ∙∙∙∙∙@∙∙∙∙∙ +∙+∙+∙+∙+∙+ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙+∙+∙+∙+∙∙ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+
+∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙+∙+∙+∙+∙∙ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ +∙+∙+∙+∙+∙+ ∙∙∙∙∙@∙∙∙∙∙ +∙+∙+∙+∙+∙+ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙+∙+∙+∙+∙∙ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+
+∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙+∙+∙+∙+∙∙ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ +∙+∙+∙+∙+∙+ ∙∙∙∙∙@∙∙∙∙∙ +∙+∙+∙+∙+∙+ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙+∙+∙+∙+∙∙ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+
+∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙+∙+∙+∙+∙∙ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ +∙+∙+∙+∙+∙+ ∙∙∙∙∙@∙∙∙∙∙ +∙+∙+∙+∙+∙+ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙+∙+∙+∙+∙∙ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+
+∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙+∙+∙+∙+∙∙ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ +∙+∙+∙+∙+∙+ ∙∙∙∙∙@∙∙∙∙∙ +∙+∙+∙+∙+∙+ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+ ∙∙∙∙∙∙∙∙∙∙∙ ∙∙+∙+∙+∙+∙∙ ∙∙∙∙∙∙∙∙∙∙∙ +∙∙∙+∙+∙∙∙+
∙∙∙∙∙∙∙∙∙∙∙∙∙+∙+∙+∙+∙ ∙+∙+∙+∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙@∙∙∙∙∙∙∙∙∙∙∙ ∙+∙+∙+∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙+∙+∙+∙+∙
∙∙∙∙∙∙∙∙∙∙∙∙∙+∙+∙+∙+∙ ∙+∙+∙+∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙@∙∙∙∙∙∙∙∙∙∙∙ ∙+∙+∙+∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙+∙+∙+∙+∙
∙∙∙∙∙∙∙∙∙∙∙∙∙+∙+∙+∙+∙ ∙+∙+∙+∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙@∙∙∙∙∙∙∙∙∙∙∙ ∙+∙+∙+∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙+∙+∙+∙+∙
∙∙∙∙∙∙∙∙∙∙∙∙∙+∙+∙+∙+∙ ∙+∙+∙+∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙@∙∙∙∙∙∙∙∙∙∙∙ ∙+∙+∙+∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙+∙+∙+∙+∙
∙∙∙∙∙∙∙∙∙∙∙∙∙+∙+∙+∙+∙ ∙+∙+∙+∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙@∙∙∙∙∙∙∙∙∙∙∙ ∙+∙+∙+∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙+∙+∙+∙+∙
∙∙∙+∙+∙∙∙+∙+∙∙∙+∙+∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙+∙+∙+∙+∙+∙+∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙+∙+∙+∙+∙+∙+∙+∙+∙+∙+∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙+@+∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙+∙+∙+∙+∙+∙+∙+∙+∙+∙+∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙+∙+∙+∙+∙+∙+∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙+∙+∙∙∙+∙+∙∙∙+∙+∙∙∙
∙∙∙+∙+∙∙∙+∙+∙∙∙+∙+∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙+∙+∙+∙+∙+∙+∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙+∙+∙+∙+∙+∙+∙+∙+∙+∙+∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙+@+∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙+∙+∙+∙+∙+∙+∙+∙+∙+∙+∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙∙∙+∙+∙+∙+∙+∙+∙∙∙∙∙ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ∙∙∙+∙+∙∙∙+∙+∙∙∙+∙+∙∙∙
∙∙∙∙+∙+∙∙∙+∙+∙∙∙+∙+∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙+∙+∙+∙+∙+∙+∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙+∙+∙+∙+∙+∙+∙+∙+∙+∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙+@+∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙+∙+∙+∙+∙+∙+∙+∙+∙+∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙+∙+∙+∙+∙+∙+∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙+∙+∙∙∙+∙+∙∙∙+∙+∙∙∙│
∙∙∙∙+∙+∙∙∙+∙+∙∙∙+∙+∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙+∙+∙+∙+∙+∙+∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙+∙+∙+∙+∙+∙+∙+∙+∙+∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙+@+∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙+∙+∙+∙+∙+∙+∙+∙+∙+∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙+∙+∙+∙+∙+∙+∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙+∙+∙∙∙+∙+∙∙∙+∙+∙∙∙│
∙∙∙∙+∙+∙∙∙+∙+∙∙∙+∙+∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙+∙+∙+∙+∙+∙+∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙+∙+∙+∙+∙+∙+∙+∙+∙+∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙+@+∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙+∙+∙+∙+∙+∙+∙+∙+∙+∙+∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙+∙+∙+∙+∙+∙+∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙+∙+∙∙∙+∙+∙∙∙+∙+∙∙∙│
Symmetrical versions
This is a comparison between the symmetrical versions of the algorithms. Ray casting is not included because it cannot be made symmetrical with reasonable efficiency. My algorithm has two symmetrical versions: one that's fully symmetrical and another that's symmetrical except for some walls (i.e. that's symmetrical between monsters except for some passwall monsters).
│∙└───────────────────┤ │∙∙∙∙∙∙∙∙∙∙@∙∙∙∙∙∙∙∙∙∙+ └───────┬┬─∙┌┬────────┤ ├┘∙∙└┤ │ ┌┘∙∙│∙└┐ │
│∙└───────────────────┤ │∙∙∙∙∙∙∙∙∙∙@∙∙∙∙∙∙∙∙∙∙+ └───────┬┬─∙┌┬────────┤ ├┘∙∙└┤ │ ┌┘∙∙│∙└┐ │
│∙└───────────────────┤ │∙∙∙∙∙∙∙∙∙∙@∙∙∙∙∙∙∙∙∙∙+ └───────┬┬─∙┌┬────────┤ ├┘∙∙└┤ │ ┌┘∙∙│∙└┐ │
│∙└───────────────────┤ │∙∙∙∙∙∙∙∙∙∙@∙∙∙∙∙∙∙∙∙∙+ └───────┬┬─∙┌┬────────┤ ├┘∙∙└┤ │ ┌┘∙∙│∙└┐ │
│∙└───────────────────┤ │∙∙∙∙∙∙∙∙∙∙@∙∙∙∙∙∙∙∙∙∙+ └───────┬┬─∙┌┬────────┤ ├┘∙∙└┤ │ ┌┘∙∙│∙└┐ │
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙ @∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ ───┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
─────┤∙∙∙∙∙∙∙┼∙∙∙┼∙
@∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙
─────┤∙∙∙∙∙∙∙┼∙∙∙┼∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙┼∙∙∙┼∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
─────┤∙∙∙∙∙∙∙┼∙∙∙┼∙
@∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙
─────┤∙∙∙∙∙∙∙┼∙∙∙┼∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙┼∙∙∙┼∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
─────┤∙∙∙∙∙∙∙┼∙∙∙┼∙
@∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙
─────┤∙∙∙∙∙∙∙┼∙∙∙┼∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙┼∙∙∙┼∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
─────┤∙∙∙∙∙∙∙┼∙∙∙┼∙
@∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙
─────┤∙∙∙∙∙∙∙┼∙∙∙┼∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙
│∙∙∙∙∙∙∙┼∙∙∙┼∙
│∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙┼∙∙∙┼∙ @∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙ ─────┤∙∙∙∙∙∙∙┼∙∙∙┼∙ │∙∙∙∙∙∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙┼∙∙∙┼∙
│ ┌───────────┐ │ │∙∙∙∙∙∙∙∙∙∙∙│ │ ┌┘∙──┬─────┐∙│ └─┬┤∙∙∙∙│ │∙│ ∙∙└┘∙∙∙∙│ │∙│ ┐∙∙∙∙∙∙∙└───┐ │∙│ └──┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙@│ │∙∙∙∙│ └─────┘
│ ┌───────────┐ │ │∙∙∙∙∙∙∙∙∙∙∙│ │ ┌┘∙──┬─────┐∙│ └─┬┤∙∙∙∙│ │∙│ ∙∙└┘∙∙∙∙│ │∙│ ┐∙∙∙∙∙∙∙└───┐ │∙│ └──┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙@│ │∙∙∙∙│ └─────┘
│ ┌───────────┐ │ │∙∙∙∙∙∙∙∙∙∙∙│ │ ┌┘∙──┬─────┐∙│ └─┬┤∙∙∙∙│ │∙│ ∙∙└┘∙∙∙∙│ │∙│ ┐∙∙∙∙∙∙∙└───┐ │∙│ └──┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙@│ │∙∙∙∙│ └─────┘
│ ┌───────────┐ │ │∙∙∙∙∙∙∙∙∙∙∙│ │ ┌┘∙──┬─────┐∙│ └─┬┤∙∙∙∙│ │∙│ ∙∙└┘∙∙∙∙│ │∙│ ┐∙∙∙∙∙∙∙└───┐ │∙│ └──┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙@│ │∙∙∙∙│ └─────┘
│ ┌───────────┐ │ │∙∙∙∙∙∙∙∙∙∙∙│ │ ┌┘∙──┬─────┐∙│ └─┬┤∙∙∙∙│ │∙│ ∙∙└┘∙∙∙∙│ │∙│ ┐∙∙∙∙∙∙∙└───┐ │∙│ └──┐∙∙∙∙∙∙∙∙└─┘∙│ │∙∙∙∙┌─┐∙∙∙∙@│ │∙∙∙∙│ └─────┘
│@└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙┼∙┼∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│∙┌┤ └────────┴─┴┘
│@└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙┼∙┼∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│∙┌┤ └────────┴─┴┘
│@└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙┼∙┼∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│∙┌┤ └────────┴─┴┘
│@└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙┼∙┼∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│∙┌┤ └────────┴─┴┘
│@└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙┼∙┼∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│∙┌┤ └────────┴─┴┘
│∙└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙┼∙┼∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│@┌┤ └────────┴─┴┘
│∙└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙┼∙┼∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│@┌┤ └────────┴─┴┘
│∙└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙┼∙┼∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│@┌┤ └────────┴─┴┘
│∙└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙┼∙┼∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│@┌┤ └────────┴─┴┘
│∙└─────────┐ │∙∙∙∙∙∙∙∙∙∙∙│ ├───∙───────┤ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙┼∙┼∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙│@┌┤ └────────┴─┴┘
┌──────── │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙┼ ┤∙∙∙∙∙∙┼∙ ■∙∙∙∙∙┼∙∙ ┤∙∙∙∙┼∙∙@
┌──────── │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙┼ ┤∙∙∙∙∙∙┼∙ ■∙∙∙∙∙┼∙∙ ┤∙∙∙∙┼∙∙@
┌──────── │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙┼ ┤∙∙∙∙∙∙┼∙ ■∙∙∙∙∙┼∙∙ ┤∙∙∙∙┼∙∙@
┌──────── │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙┼ ┤∙∙∙∙∙∙┼∙ ■∙∙∙∙∙┼∙∙ ┤∙∙∙∙┼∙∙@
┌──────── │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙┼ ┤∙∙∙∙∙∙┼∙ ■∙∙∙∙∙┼∙∙ ┤∙∙∙∙┼∙∙@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙┼ ┤∙∙∙∙∙┼∙ ■∙∙∙∙┼∙@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙┼ ┤∙∙∙∙∙┼∙ ■∙∙∙∙┼∙@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙┼ ┤∙∙∙∙∙┼∙ ■∙∙∙∙┼∙@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙┼ ┤∙∙∙∙∙┼∙ ■∙∙∙∙┼∙@
┌─────── │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙∙ │∙∙∙∙∙∙┼ ┤∙∙∙∙∙┼∙ ■∙∙∙∙┼∙@
┌───────────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙∙∙│ ■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ ┤∙∙∙∙∙∙∙┼∙@∙┼∙∙∙∙∙∙∙■ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ │∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┴─────────+─────────┴
┌───────────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙∙∙│ ■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ ┤∙∙∙∙∙∙∙┼∙@∙┼∙∙∙∙∙∙∙■ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ │∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┴─────────+─────────┴
┌───────────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙∙∙│ ■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ ┤∙∙∙∙∙∙∙┼∙@∙┼∙∙∙∙∙∙∙■ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ │∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┴─────────+─────────┴
┌───────────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙∙∙│ ■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ ┤∙∙∙∙∙∙∙┼∙@∙┼∙∙∙∙∙∙∙■ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ │∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┴─────────+─────────┴
┌───────────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┤∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙∙∙│ ■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ ┤∙∙∙∙∙∙∙┼∙@∙┼∙∙∙∙∙∙∙■ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙├ │∙∙∙∙∙∙∙┼∙∙∙┼∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ┴─────────+─────────┴
──────────────┐ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙├ @∙∙∙∙∙∙∙∙∙∙∙∙∙+ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙├ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ────────+─────┤
──────────────┐ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙├ @∙∙∙∙∙∙∙∙∙∙∙∙∙+ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙├ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ────────+─────┤
──────────────┐ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙├ @∙∙∙∙∙∙∙∙∙∙∙∙∙+ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙├ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ────────+─────┤
──────────────┐ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙├ @∙∙∙∙∙∙∙∙∙∙∙∙∙+ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙├ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ────────+─────┤
──────────────┐ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙├ @∙∙∙∙∙∙∙∙∙∙∙∙∙+ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙├ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ∙∙┼∙∙∙∙∙∙∙∙∙∙∙│ ∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ ────────+─────┤
Performance
Here's a table describing the performance of the algorithms in various scenarios. Higher numbers are better, although what matters is the performance ratio between the algorithms, not the absolute numbers. (The absolute numbers represent the number of executions per second on a single core on my machine.)| Map | Ray casting | Shadow casting | Diamond walls | My algorithm | Permissive FOV |
|---|---|---|---|---|---|
| Empty (20x20) | 83608 | 89577 | 86875 | 60369 | 12023 |
| Empty (100x100) | 3404 | 4910 | 4886 | 3357 | 686 |
| Empty (r4) | 292667 | 370378 | 353276 | 280859 | 47114 |
| Empty (r8) | 81312 | 132148 | 111511 | 99660 | 21480 |
| Outdoor (20x20) | 139177 | 174070 | 94148 | 66163 | 17513 |
| Outdoor (100x100) | 24962 | 140925 | 48697 | 39168 | 9695 |
| Outdoor (r4) | 335738 | 415981 | 316644 | 238420 | 52208 |
| Outdoor (r8) | 124778 | 203971 | 133292 | 100906 | 27004 |
| Short corridor (120x65) | 48772 | 436706 | 319513 | 213801 | 37914 |
| Long corridor (120x65) | 56706 | 201857 | 143236 | 96420 | 12217 |
| Corridor (r4) | 547637 | 826194 | 663561 | 481718 | 85724 |
| Corridor (r8) | 269678 | 501827 | 392415 | 269976 | 45214 |
| Twisty (120x65) | 92842 | 917276 | 642697 | 449043 | 93691 |
| Pillars 1 (120x65) | 24500 | 127665 | 85191 | 55416 | 13975 |
| Pillars 1 (r4) | 305107 | 358532 | 308018 | 214630 | 45589 |
| Pillars 1 (r8) | 106697 | 161567 | 120698 | 85148 | 24007 |
| Pillars 2 (r4) | 417075 | 533839 | 328767 | 228298 | 63121 |
| Pillars 2 (r8) | 195550 | 288526 | 141408 | 133588 | 32876 |
| Room (120x65) | 39478 | 398466 | 250948 | 152344 | 30615 |
| Room (r4) | 329058 | 417253 | 364965 | 260983 | 61807 |
| Room (r8) | 154439 | 334664 | 276130 | 191062 | 46470 |
| Avg. speed factor | 52% | 100% | 78% | 53% | 11% |
- Empty maps are simply empty space with no obstacles.
- Outdoor maps are maps with 25% of the space being randomly placed obstacles (wall tiles).
- R4 and r8 refer to algorithms run with the maximum sight radius set to 4 or 8, while AxB refers to the width and height of the map and implies an unlimited sight radius. The size of the map or sight radius has the largest effect on ray casting, since it must always cast a number of rays proportional to the map size or sight radius.
- Green cells are at least 75% of the speed of the fastest algorithm. Yellow cells are at least half its speed but less than 75%. Orange cells are at least one third its speed but less than half. Red cells are less than one third.
It seems that I didn't quite reach my goal of having speed on par with the diagonal walls algorithm, but I succeeded in all other goals. My algorithm is only about 2/3rds the speed of the diagonal walls algorithm, but it should be fast enough for almost any game. Furthermore, there is still significant optimization that could be done.
Code
This class, Visibility, defines the interface used by all algorithms.abstract class Visibility
{
/// <param name="origin">The location of the monster whose field of view will be calculated.</param>
/// <param name="rangeLimit">The maximum distance from the origin that tiles will be lit.
/// If equal to -1, no limit will be applied.
/// </param>
public abstract void Compute(LevelPoint origin, int rangeLimit);
}
Ray casting
Here's the code for ray casting, assuming the map is no larger than 65536 tiles across and with error-checking elided. Rather than hard-code any particular method for representing the map, checking for opacity, or computing distances, the code accepts pointers to functions that handle these details.sealed class RayCastVisibility : Visibility
{
/// <param name="mapSize">The size of the map.</param>
/// <param name="blocksLight">A function that accepts the X and Y coordinates of a tile and determines
/// whether the given tile blocks the passage of light.
/// </param>
/// <param name="setVisible">A function that sets a tile to be visible, given its X and Y coordinates.</param>
/// <param name="getDistance">A function that a pair of X and Y coordinates and returns the distance
/// between the two points.
/// </param>
public RayCastVisibility(Size mapSize, Func<int,int,bool> blocksLight, Action<int,int> setVisible,
Func<int,int,int,int,int> getDistance)
{
MapSize = mapSize;
BlocksLight = blocksLight;
SetVisible = setVisible;
GetDistance = getDistance;
}
public override void Compute(LevelPoint origin, int rangeLimit)
{
SetVisible(origin.X, origin.Y);
if(rangeLimit != 0)
{
Rectangle area = new Rectangle(0, 0, MapSize.Width, MapSize.Height); // cast to the edge of the map by default
if(rangeLimit >= 0) // but limit the area to the rectangle containing the sight radius if one was provided
{
area.Intersect(new Rectangle(origin.X-rangeLimit, origin.Y-rangeLimit, rangeLimit*2+1, rangeLimit*2+1));
}
for(int x=area.Left; x<area.Right; x++) // cast rays towards the top and bottom of the area
{
TraceLine(origin, x, area.Top, rangeLimit);
TraceLine(origin, x, area.Bottom-1, rangeLimit);
}
for(int y=area.Top+1; y<area.Bottom-1; y++) // and to the left and right
{
TraceLine(origin, area.Left, y, rangeLimit);
TraceLine(origin, area.Right-1, y, rangeLimit);
}
}
}
void TraceLine(LevelPoint origin, int x2, int y2, int rangeLimit)
{
int xDiff = x2 - origin.X, yDiff = y2 - origin.Y, xLen = Math.Abs(xDiff), yLen = Math.Abs(yDiff);
int xInc = Math.Sign(xDiff), yInc = Math.Sign(yDiff)<<16, index = (origin.Y<<16) + origin.X;
if(xLen < yLen) // make sure we walk along the long axis
{
Utility.Swap(ref xLen, ref yLen);
Utility.Swap(ref xInc, ref yInc);
}
int errorInc = yLen*2, error = -xLen, errorReset = xLen*2;
while(--xLen >= 0) // skip the first point (the origin) since it's always visible and should never stop rays
{
index += xInc; // advance down the long axis (could be X or Y)
error += errorInc;
if(error > 0) { error -= errorReset; index += yInc; }
int x = index & 0xFFFF, y = index >> 16;
if(rangeLimit >= 0 && GetDistance(origin.X, origin.Y, x, y) > rangeLimit) break;
SetVisible(x, y);
if(BlocksLight(x, y)) break;
}
}
readonly Size MapSize;
readonly Func<int, int, bool> BlocksLight;
readonly Func<int, int, int, int, int> GetDistance;
readonly Action<int, int> SetVisible;
}
Shadow casting
Here's the code for basic, asymmetrical shadow casting with square tiles. See the "NOTE:" comment for a simple change you can make if you want the algorithm to be symmetrical.sealed class ShadowCastVisibility : Visibility
{
/// <param name="blocksLight">A function that accepts the X and Y coordinates of a tile and determines whether the
/// given tile blocks the passage of light. The function must be able to accept coordinates that are out of bounds.
/// </param>
/// <param name="setVisible">A function that sets a tile to be visible, given its X and Y coordinates. The function
/// must ignore coordinates that are out of bounds.
/// </param>
/// <param name="getDistance">A function that takes the X and Y coordinate of a point where X >= 0,
/// Y >= 0, and X >= Y, and returns the distance from the point to the origin.
/// </param>
public ShadowCastVisibility(Func<int, int, bool> blocksLight, Action<int, int> setVisible,
Func<int,int,int> getDistance)
{
BlocksLight = blocksLight;
GetDistance = getDistance;
SetVisible = setVisible;
}
public override void Compute(LevelPoint origin, int rangeLimit)
{
SetVisible(origin.X, origin.Y);
for(uint octant=0; octant<8; octant++) Compute(octant, origin, rangeLimit, 1, new Slope(1, 1), new Slope(0, 1));
}
struct Slope // represents the slope Y/X as a rational number
{
public Slope(int y, int x) { Y=y; X=x; }
public readonly int Y, X;
}
void Compute(uint octant, LevelPoint origin, int rangeLimit, int x, Slope top, Slope bottom)
{
for(; (uint)x <= (uint)rangeLimit; x++) // rangeLimit < 0 || x <= rangeLimit
{
// compute the Y coordinates where the top vector leaves the column (on the right) and where the bottom vector
// enters the column (on the left). this equals (x+0.5)*top+0.5 and (x-0.5)*bottom+0.5 respectively, which can
// be computed like (x+0.5)*top+0.5 = (2(x+0.5)*top+1)/2 = ((2x+1)*top+1)/2 to avoid floating point math
int topY = top.X == 1 ? x : ((x*2+1) * top.Y + top.X - 1) / (top.X*2); // the rounding is a bit tricky, though
int bottomY = bottom.Y == 0 ? 0 : ((x*2-1) * bottom.Y + bottom.X) / (bottom.X*2);
int wasOpaque = -1; // 0:false, 1:true, -1:not applicable
for(int y=topY; y >= bottomY; y--)
{
int tx = origin.X, ty = origin.Y;
switch(octant) // translate local coordinates to map coordinates
{
case 0: tx += x; ty -= y; break;
case 1: tx += y; ty -= x; break;
case 2: tx -= y; ty -= x; break;
case 3: tx -= x; ty -= y; break;
case 4: tx -= x; ty += y; break;
case 5: tx -= y; ty += x; break;
case 6: tx += y; ty += x; break;
case 7: tx += x; ty += y; break;
}
bool inRange = rangeLimit < 0 || GetDistance(x, y) <= rangeLimit;
if(inRange) SetVisible(tx, ty);
// NOTE: use the next line instead if you want the algorithm to be symmetrical
// if(inRange && (y != topY || top.Y*x >= top.X*y) && (y != bottomY || bottom.Y*x <= bottom.X*y)) SetVisible(tx, ty);
bool isOpaque = !inRange || BlocksLight(tx, ty);
if(x != rangeLimit)
{
if(isOpaque)
{
if(wasOpaque == 0) // if we found a transition from clear to opaque, this sector is done in this column, so
{ // adjust the bottom vector upwards and continue processing it in the next column.
Slope newBottom = new Slope(y*2+1, x*2-1); // (x*2-1, y*2+1) is a vector to the top-left of the opaque tile
if(!inRange || y == bottomY) { bottom = newBottom; break; } // don't recurse unless we have to
else Compute(octant, origin, rangeLimit, x+1, top, newBottom);
}
wasOpaque = 1;
}
else // adjust top vector downwards and continue if we found a transition from opaque to clear
{ // (x*2+1, y*2+1) is the top-right corner of the clear tile (i.e. the bottom-right of the opaque tile)
if(wasOpaque > 0) top = new Slope(y*2+1, x*2+1);
wasOpaque = 0;
}
}
}
if(wasOpaque != 0) break; // if the column ended in a clear tile, continue processing the current sector
}
}
readonly Func<int, int, bool> BlocksLight;
readonly Func<int, int, int> GetDistance;
readonly Action<int, int> SetVisible;
}
Diamond walls
Here is code to implement the diamond walls algorithm. As before, see the "NOTE:" comment for a simple change that will make the algorithm symmetrical.sealed class DiamondWallsVisibility : Visibility
{
/// <param name="blocksLight">A function that accepts the X and Y coordinates of a tile and determines
/// whether the given tile blocks the passage of light.
/// </param>
/// <param name="setVisible">A function that sets a tile to be visible, given its X and Y coordinates.</param>
/// <param name="getDistance">A function that takes the X and Y coordinate of a point where X >= 0,
/// Y >= 0, and X >= Y, and returns the distance from the point to the origin (0,0).
/// </param>
public DiamondWallsVisibility(Func<int,int,bool> blocksLight, Action<int,int> setVisible,
Func<int,int,int> getDistance)
{
_blocksLight = blocksLight;
GetDistance = getDistance;
SetVisible = setVisible;
}
public override void Compute(LevelPoint origin, int rangeLimit)
{
SetVisible(origin.X, origin.Y);
for(uint octant=0; octant<8; octant++) Compute(octant, origin, rangeLimit, 1, new Slope(1, 1), new Slope(0, 1));
}
struct Slope // represents the slope Y/X as a rational number
{
public Slope(int y, int x) { Y=y; X=x; }
public bool Greater(int y, int x) { return Y*x > X*y; } // this > y/x
public bool GreaterOrEqual(int y, int x) { return Y*x >= X*y; } // this >= y/x
public bool LessOrEqual(int y, int x) { return Y*x <= X*y; } // this <= y/x
public readonly int Y, X;
}
void Compute(uint octant, LevelPoint origin, int rangeLimit, int x, Slope top, Slope bottom)
{
for(; (uint)x <= (uint)rangeLimit; x++) // rangeLimit < 0 || x <= rangeLimit
{
int topY;
if(top.X == 1)
{
topY = x;
}
else
{
topY = ((x*2-1) * top.Y + top.X) / (top.X*2); // get the tile that the top vector enters from the left
int ay = (topY*2+1) * top.X;
if(BlocksLight(x, topY, octant, origin)) // if the top tile is a wall...
{
if(top.GreaterOrEqual(ay, x*2)) topY++; // but the top vector misses the wall and passes into the tile above, move up
}
else // the top tile is not a wall
{
if(top.Greater(ay, x*2+1)) topY++; // so if the top vector passes into the tile above, move up
}
}
int bottomY = bottom.Y == 0 ? 0 : ((x*2-1) * bottom.Y + bottom.X) / (bottom.X*2);
int wasOpaque = -1; // 0:false, 1:true, -1:not applicable
for(int y=topY; y >= bottomY; y--)
{
int tx = origin.X, ty = origin.Y;
switch(octant) // translate local coordinates to map coordinates
{
case 0: tx += x; ty -= y; break;
case 1: tx += y; ty -= x; break;
case 2: tx -= y; ty -= x; break;
case 3: tx -= x; ty -= y; break;
case 4: tx -= x; ty += y; break;
case 5: tx -= y; ty += x; break;
case 6: tx += y; ty += x; break;
case 7: tx += x; ty += y; break;
}
bool inRange = rangeLimit < 0 || GetDistance(x, y) <= rangeLimit;
// NOTE: use the following line instead to make the algorithm symmetrical
// if(inRange && (y != topY || top.GreaterOrEqual(y, x)) && (y != bottomY || bottom.LessOrEqual(y, x))) SetVisible(tx, ty);
if(inRange) SetVisible(tx, ty);
bool isOpaque = !inRange || _blocksLight(tx, ty);
// if y == topY or y == bottomY, make sure the sector actually intersects the wall tile. if not, don't consider
// it opaque to prevent the code below from moving the top vector up or the bottom vector down
if(isOpaque &&
(y == topY && top.LessOrEqual(y*2-1, x*2) && !BlocksLight(x, y-1, octant, origin) ||
y == bottomY && bottom.GreaterOrEqual(y*2+1, x*2) && !BlocksLight(x, y+1, octant, origin)))
{
isOpaque = false;
}
if(x != rangeLimit)
{
if(isOpaque)
{
if(wasOpaque == 0) // if we found a transition from clear to opaque, this sector is done in this column, so
{ // adjust the bottom vector upwards and continue processing it in the next column.
// (x*2-1, y*2+1) is a vector to the top-left corner of the opaque block
if(!inRange || y == bottomY) { bottom = new Slope(y*2+1, x*2); break; } // don't recurse unless necessary
else Compute(octant, origin, rangeLimit, x+1, top, new Slope(y*2+1, x*2));
}
wasOpaque = 1;
}
else // adjust the top vector downwards and continue if we found a transition from opaque to clear
{ // (x*2+1, y*2+1) is the top-right corner of the clear tile (i.e. the bottom-right of the opaque tile)
if(wasOpaque > 0) top = new Slope(y*2+1, x*2);
wasOpaque = 0;
}
}
}
if(wasOpaque != 0) break; // if the column ended in a clear tile, continue processing the current sector
}
}
bool BlocksLight(int x, int y, uint octant, LevelPoint origin)
{
int nx = origin.X, ny = origin.Y;
switch(octant)
{
case 0: nx += x; ny -= y; break;
case 1: nx += y; ny -= x; break;
case 2: nx -= y; ny -= x; break;
case 3: nx -= x; ny -= y; break;
case 4: nx -= x; ny += y; break;
case 5: nx -= y; ny += x; break;
case 6: nx += y; ny += x; break;
case 7: nx += x; ny += y; break;
}
return _blocksLight(nx, ny);
}
readonly Func<int, int, bool> _blocksLight;
readonly Func<int, int, int> GetDistance;
readonly Action<int, int> SetVisible;
}
Permissive field of view
Here is code to implement the permissive field of view algorithm. This code was adapted from a demo by Jonathon Duerig. The permissive field of view algorithm is always symmetrical.sealed class PermissiveVisibility : Visibility
{
/// <param name="blocksLight">A function that accepts the X and Y coordinates of a tile and determines
/// whether the given tile blocks the passage of light.
/// </param>
/// <param name="setVisible">A function that sets a tile to be visible, given its X and Y coordinates.</param>
/// <param name="getDistance">A function that takes the X and Y coordinate of a point where X >= 0,
/// Y >= 0, and X >= Y, and returns the distance from the point to the origin (0,0).
/// </param>
public PermissiveVisibility(Func<int,int,bool> blocksLight, Action<int,int> setVisible,
Func<int,int,int> getDistance)
{
BlocksLight = blocksLight;
SetVisible = setVisible;
GetDistance = getDistance;
}
public override void Compute(LevelPoint origin, int rangeLimit)
{
source = new Offset(origin.X, origin.Y);
this.rangeLimit = rangeLimit;
for(int q=0; q<4; q++)
{
quadrant.x = (short)(q == 0 || q == 3 ? 1 : -1);
quadrant.y = (short)(q < 2 ? 1 : -1);
ComputeQuadrant();
}
}
sealed class Bump
{
public Bump parent;
public Offset location;
}
struct Field
{
public Bump steepBump, shallowBump;
public Line steep, shallow;
}
struct Line
{
public Line(Offset near, Offset far) { this.near = near; this.far = far; }
public Offset near, far;
public bool isBelow(Offset point)
{
return relativeSlope(point) > 0;
}
public bool isBelowOrContains(Offset point)
{
return relativeSlope(point) >= 0;
}
public bool isAbove(Offset point)
{
return relativeSlope(point) < 0;
}
public bool isAboveOrContains(Offset point)
{
return relativeSlope(point) <= 0;
}
public bool doesContain(Offset point)
{
return relativeSlope(point) == 0;
}
// negative if the line is above the point.
// positive if the line is below the point.
// 0 if the line is on the point.
public int relativeSlope(Offset point)
{
return (far.y - near.y)*(far.x - point.x) - (far.y - point.y)*(far.x - near.x);
}
}
struct Offset
{
public Offset(int x, int y) { this.x = (short)x; this.y = (short)y; }
public short x, y;
}
void ComputeQuadrant()
{
const int Infinity = short.MaxValue;
LinkedList<Field> activeFields = new LinkedList<Field>();
activeFields.AddLast(new Field() { steep = new Line(new Offset(1, 0), new Offset(0, Infinity)), shallow = new Line(new Offset(0, 1), new Offset(Infinity, 0)) });
Offset dest = new Offset();
actIsBlocked(dest);
for(int i=1; i<Infinity && activeFields.Count != 0; i++)
{
LinkedListNode<Field> current = activeFields.First;
for(int j=0; j <= i; j++)
{
dest.x = (short)(i-j);
dest.y = (short)j;
current = visitSquare(dest, current, activeFields);
}
}
}
bool actIsBlocked(Offset pos)
{
if(rangeLimit >= 0 && GetDistance(Math.Max(pos.x, pos.y), Math.Min(pos.x, pos.y)) > rangeLimit) return true;
int x = pos.x*quadrant.x + source.x, y = pos.y*quadrant.y + source.y;
SetVisible(x, y);
return BlocksLight(x, y);
}
LinkedListNode<Field> visitSquare(Offset dest, LinkedListNode<Field> currentField, LinkedList<Field> activeFields)
{
Offset topLeft = new Offset(dest.x, dest.y+1), bottomRight = new Offset(dest.x+1, dest.y);
while(currentField != null && currentField.Value.steep.isBelowOrContains(bottomRight)) currentField = currentField.Next;
if(currentField == null || currentField.Value.shallow.isAboveOrContains(topLeft) || !actIsBlocked(dest)) return currentField;
if(currentField.Value.shallow.isAbove(bottomRight) && currentField.Value.steep.isBelow(topLeft))
{
LinkedListNode<Field> next = currentField.Next;
activeFields.Remove(currentField);
return next;
}
else if(currentField.Value.shallow.isAbove(bottomRight))
{
addShallowBump(topLeft, currentField);
return checkField(currentField, activeFields);
}
else if(currentField.Value.steep.isBelow(topLeft))
{
addSteepBump(bottomRight, currentField);
return checkField(currentField, activeFields);
}
else
{
LinkedListNode<Field> steeper = currentField, shallower = activeFields.AddBefore(currentField, currentField.Value);
addSteepBump(bottomRight, shallower);
checkField(shallower, activeFields);
addShallowBump(topLeft, steeper);
return checkField(steeper, activeFields);
}
}
static void addShallowBump(Offset point, LinkedListNode<Field> currentField)
{
Field value = currentField.Value;
value.shallow.far = point;
value.shallowBump = new Bump() { location = point, parent = value.shallowBump };
Bump currentBump = value.steepBump;
while(currentBump != null)
{
if(value.shallow.isAbove(currentBump.location)) value.shallow.near = currentBump.location;
currentBump = currentBump.parent;
}
currentField.Value = value;
}
static void addSteepBump(Offset point, LinkedListNode<Field> currentField)
{
Field value = currentField.Value;
value.steep.far = point;
value.steepBump = new Bump() { location = point, parent = value.steepBump };
// Now look through the list of shallow bumps and see if any of them are below the line.
for(Bump currentBump = value.shallowBump; currentBump != null; currentBump = currentBump.parent)
{
if (value.steep.isBelow(currentBump.location)) value.steep.near = currentBump.location;
}
currentField.Value = value;
}
static LinkedListNode<Field> checkField(LinkedListNode<Field> currentField, LinkedList<Field> activeFields)
{
LinkedListNode<Field> result = currentField;
if(currentField.Value.shallow.doesContain(currentField.Value.steep.near) &&
currentField.Value.shallow.doesContain(currentField.Value.steep.far) &&
(currentField.Value.shallow.doesContain(new Offset(0, 1)) || currentField.Value.shallow.doesContain(new Offset(1, 0))))
{
result = currentField.Next;
activeFields.Remove(currentField);
}
return result;
}
readonly Func<int, int, bool> BlocksLight;
readonly Func<int, int, int> GetDistance;
readonly Action<int, int> SetVisible;
Offset source, quadrant;
int rangeLimit;
}
My algorithm
Here the code to implement my own visibility algorithm. It's long, but it's mostly comments. See the "NOTE:" comments for changes that can be made to make the algorithm mostly or fully symmetrical. Although it's fairly well optimized, there is still a significant improvement that could be made. If the map stored a bit mask for each tile indicating whether each of the corners was beveled, most of the calls to BlocksLight could be removed.sealed class MyVisibility : Visibility
{
/// <param name="blocksLight">A function that accepts the X and Y coordinates of a tile and determines whether the
/// given tile blocks the passage of light. The function must be able to accept coordinates that are out of bounds.
/// </param>
/// <param name="setVisible">A function that sets a tile to be visible, given its X and Y coordinates. The function
/// must ignore coordinates that are out of bounds.
/// </param>
/// <param name="getDistance">A function that takes the X and Y coordinate of a point where X >= 0,
/// Y >= 0, and X >= Y, and returns the distance from the point to the origin (0,0).
/// </param>
public MyVisibility(Func<int, int, bool> blocksLight, Action<int, int> setVisible, Func<int, int, int> getDistance)
{
_blocksLight = blocksLight;
GetDistance = getDistance;
_setVisible = setVisible;
}
public override void Compute(LevelPoint origin, int rangeLimit)
{
_setVisible(origin.X, origin.Y);
for(uint octant=0; octant<8; octant++) Compute(octant, origin, rangeLimit, 1, new Slope(1, 1), new Slope(0, 1));
}
struct Slope // represents the slope Y/X as a rational number
{
public Slope(uint y, uint x) { Y = y; X = x; }
public bool Greater(uint y, uint x) { return Y*x > X*y; } // this > y/x
public bool GreaterOrEqual(uint y, uint x) { return Y*x >= X*y; } // this >= y/x
public bool Less(uint y, uint x) { return Y*x < X*y; } // this < y/x
//public bool LessOrEqual(uint y, uint x) { return Y*x <= X*y; } // this <= y/x
public readonly uint X, Y;
}
void Compute(uint octant, LevelPoint origin, int rangeLimit, uint x, Slope top, Slope bottom)
{
// throughout this function there are references to various parts of tiles. a tile's coordinates refer to its
// center, and the following diagram shows the parts of the tile and the vectors from the origin that pass through
// those parts. given a part of a tile with vector u, a vector v passes above it if v > u and below it if v < u
// g center: y / x
// a------b a top left: (y*2+1) / (x*2-1) i inner top left: (y*4+1) / (x*4-1)
// | /\ | b top right: (y*2+1) / (x*2+1) j inner top right: (y*4+1) / (x*4+1)
// |i/__\j| c bottom left: (y*2-1) / (x*2-1) k inner bottom left: (y*4-1) / (x*4-1)
//e|/| |\|f d bottom right: (y*2-1) / (x*2+1) m inner bottom right: (y*4-1) / (x*4+1)
// |\|__|/| e middle left: (y*2) / (x*2-1)
// |k\ /m| f middle right: (y*2) / (x*2+1) a-d are the corners of the tile
// | \/ | g top center: (y*2+1) / (x*2) e-h are the corners of the inner (wall) diamond
// c------d h bottom center: (y*2-1) / (x*2) i-m are the corners of the inner square (1/2 tile width)
// h
for(; x <= (uint)rangeLimit; x++) // (x <= (uint)rangeLimit) == (rangeLimit < 0 || x <= rangeLimit)
{
// compute the Y coordinates of the top and bottom of the sector. we maintain that top > bottom
uint topY;
if(top.X == 1) // if top == ?/1 then it must be 1/1 because 0/1 < top <= 1/1. this is special-cased because top
{ // starts at 1/1 and remains 1/1 as long as it doesn't hit anything, so it's a common case
topY = x;
}
else // top < 1
{
// get the tile that the top vector enters from the left. since our coordinates refer to the center of the
// tile, this is (x-0.5)*top+0.5, which can be computed as (x-0.5)*top+0.5 = (2(x+0.5)*top+1)/2 =
// ((2x+1)*top+1)/2. since top == a/b, this is ((2x+1)*a+b)/2b. if it enters a tile at one of the left
// corners, it will round up, so it'll enter from the bottom-left and never the top-left
topY = ((x*2-1) * top.Y + top.X) / (top.X*2); // the Y coordinate of the tile entered from the left
// now it's possible that the vector passes from the left side of the tile up into the tile above before
// exiting from the right side of this column. so we may need to increment topY
if(BlocksLight(x, topY, octant, origin)) // if the tile blocks light (i.e. is a wall)...
{
// if the tile entered from the left blocks light, whether it passes into the tile above depends on the shape
// of the wall tile as well as the angle of the vector. if the tile has does not have a beveled top-left
// corner, then it is blocked. the corner is beveled if the tiles above and to the left are not walls. we can
// ignore the tile to the left because if it was a wall tile, the top vector must have entered this tile from
// the bottom-left corner, in which case it can't possibly enter the tile above.
//
// otherwise, with a beveled top-left corner, the slope of the vector must be greater than or equal to the
// slope of the vector to the top center of the tile (x*2, topY*2+1) in order for it to miss the wall and
// pass into the tile above
if(top.GreaterOrEqual(topY*2+1, x*2) && !BlocksLight(x, topY+1, octant, origin)) topY++;
}
else // the tile doesn't block light
{
// since this tile doesn't block light, there's nothing to stop it from passing into the tile above, and it
// does so if the vector is greater than the vector for the bottom-right corner of the tile above. however,
// there is one additional consideration. later code in this method assumes that if a tile blocks light then
// it must be visible, so if the tile above blocks light we have to make sure the light actually impacts the
// wall shape. now there are three cases: 1) the tile above is clear, in which case the vector must be above
// the bottom-right corner of the tile above, 2) the tile above blocks light and does not have a beveled
// bottom-right corner, in which case the vector must be above the bottom-right corner, and 3) the tile above
// blocks light and does have a beveled bottom-right corner, in which case the vector must be above the
// bottom center of the tile above (i.e. the corner of the beveled edge).
//
// now it's possible to merge 1 and 2 into a single check, and we get the following: if the tile above and to
// the right is a wall, then the vector must be above the bottom-right corner. otherwise, the vector must be
// above the bottom center. this works because if the tile above and to the right is a wall, then there are
// two cases: 1) the tile above is also a wall, in which case we must check against the bottom-right corner,
// or 2) the tile above is not a wall, in which case the vector passes into it if it's above the bottom-right
// corner. so either way we use the bottom-right corner in that case. now, if the tile above and to the right
// is not a wall, then we again have two cases: 1) the tile above is a wall with a beveled edge, in which
// case we must check against the bottom center, or 2) the tile above is not a wall, in which case it will
// only be visible if light passes through the inner square, and the inner square is guaranteed to be no
// larger than a wall diamond, so if it wouldn't pass through a wall diamond then it can't be visible, so
// there's no point in incrementing topY even if light passes through the corner of the tile above. so we
// might as well use the bottom center for both cases.
uint ax = x*2; // center
if(BlocksLight(x+1, topY+1, octant, origin)) ax++; // use bottom-right if the tile above and right is a wall
if(top.Greater(topY*2+1, ax)) topY++;
}
}
uint bottomY;
if(bottom.Y == 0) // if bottom == 0/?, then it's hitting the tile at Y=0 dead center. this is special-cased because
{ // bottom.Y starts at zero and remains zero as long as it doesn't hit anything, so it's common
bottomY = 0;
}
else // bottom > 0
{
bottomY = ((x*2-1) * bottom.Y + bottom.X) / (bottom.X*2); // the tile that the bottom vector enters from the left
// code below assumes that if a tile is a wall then it's visible, so if the tile contains a wall we have to
// ensure that the bottom vector actually hits the wall shape. it misses the wall shape if the top-left corner
// is beveled and bottom >= (bottomY*2+1)/(x*2). finally, the top-left corner is beveled if the tiles to the
// left and above are clear. we can assume the tile to the left is clear because otherwise the bottom vector
// would be greater, so we only have to check above
if(bottom.GreaterOrEqual(bottomY*2+1, x*2) && BlocksLight(x, bottomY, octant, origin) &&
!BlocksLight(x, bottomY+1, octant, origin))
{
bottomY++;
}
}
// go through the tiles in the column now that we know which ones could possibly be visible
int wasOpaque = -1; // 0:false, 1:true, -1:not applicable
for(uint y = topY; (int)y >= (int)bottomY; y--) // use a signed comparison because y can wrap around when decremented
{
if(rangeLimit < 0 || GetDistance((int)x, (int)y) <= rangeLimit) // skip the tile if it's out of visual range
{
bool isOpaque = BlocksLight(x, y, octant, origin);
// every tile where topY > y > bottomY is guaranteed to be visible. also, the code that initializes topY and
// bottomY guarantees that if the tile is opaque then it's visible. so we only have to do extra work for the
// case where the tile is clear and y == topY or y == bottomY. if y == topY then we have to make sure that
// the top vector is above the bottom-right corner of the inner square. if y == bottomY then we have to make
// sure that the bottom vector is below the top-left corner of the inner square
bool isVisible =
isOpaque || ((y != topY || top.Greater(y*4-1, x*4+1)) && (y != bottomY || bottom.Less(y*4+1, x*4-1)));
// NOTE: if you want the algorithm to be either fully or mostly symmetrical, replace the line above with the
// following line (and uncomment the Slope.LessOrEqual method). the line ensures that a clear tile is visible
// only if there's an unobstructed line to its center. if you want it to be fully symmetrical, also remove
// the "isOpaque ||" part and see NOTE comments further down
// bool isVisible = isOpaque || ((y != topY || top.GreaterOrEqual(y, x)) && (y != bottomY || bottom.LessOrEqual(y, x)));
if(isVisible) SetVisible(x, y, octant, origin);
// if we found a transition from clear to opaque or vice versa, adjust the top and bottom vectors
if(x != rangeLimit) // but don't bother adjusting them if this is the last column anyway
{
if(isOpaque)
{
if(wasOpaque == 0) // if we found a transition from clear to opaque, this sector is done in this column,
{ // so adjust the bottom vector upward and continue processing it in the next column
// if the opaque tile has a beveled top-left corner, move the bottom vector up to the top center.
// otherwise, move it up to the top left. the corner is beveled if the tiles above and to the left are
// clear. we can assume the tile to the left is clear because otherwise the vector would be higher, so
// we only have to check the tile above
uint nx = x*2, ny = y*2+1; // top center by default
// NOTE: if you're using full symmetry and want more expansive walls (recommended), comment out the next line
if(BlocksLight(x, y+1, octant, origin)) nx--; // top left if the corner is not beveled
if(top.Greater(ny, nx)) // we have to maintain the invariant that top > bottom, so the new sector
{ // created by adjusting the bottom is only valid if that's the case
// if we're at the bottom of the column, then just adjust the current sector rather than recursing
// since there's no chance that this sector can be split in two by a later transition back to clear
if(y == bottomY) { bottom = new Slope(ny, nx); break; } // don't recurse unless necessary
else Compute(octant, origin, rangeLimit, x+1, top, new Slope(ny, nx));
}
else // the new bottom is greater than or equal to the top, so the new sector is empty and we'll ignore
{ // it. if we're at the bottom of the column, we'd normally adjust the current sector rather than
if(y == bottomY) return; // recursing, so that invalidates the current sector and we're done
}
}
wasOpaque = 1;
}
else
{
if(wasOpaque > 0) // if we found a transition from opaque to clear, adjust the top vector downwards
{
// if the opaque tile has a beveled bottom-right corner, move the top vector down to the bottom center.
// otherwise, move it down to the bottom right. the corner is beveled if the tiles below and to the right
// are clear. we know the tile below is clear because that's the current tile, so just check to the right
uint nx = x*2, ny = y*2+1; // the bottom of the opaque tile (oy*2-1) equals the top of this tile (y*2+1)
// NOTE: if you're using full symmetry and want more expansive walls (recommended), comment out the next line
if(BlocksLight(x+1, y+1, octant, origin)) nx++; // check the right of the opaque tile (y+1), not this one
// we have to maintain the invariant that top > bottom. if not, the sector is empty and we're done
if(bottom.GreaterOrEqual(ny, nx)) return;
top = new Slope(ny, nx);
}
wasOpaque = 0;
}
}
}
}
// if the column didn't end in a clear tile, then there's no reason to continue processing the current sector
// because that means either 1) wasOpaque == -1, implying that the sector is empty or at its range limit, or 2)
// wasOpaque == 1, implying that we found a transition from clear to opaque and we recursed and we never found
// a transition back to clear, so there's nothing else for us to do that the recursive method hasn't already. (if
// we didn't recurse (because y == bottomY), it would have executed a break, leaving wasOpaque equal to 0.)
if(wasOpaque != 0) break;
}
}
// NOTE: the code duplication between BlocksLight and SetVisible is for performance. don't refactor the octant
// translation out unless you don't mind an 18% drop in speed
bool BlocksLight(uint x, uint y, uint octant, LevelPoint origin)
{
uint nx = (uint)origin.X, ny = (uint)origin.Y;
switch(octant)
{
case 0: nx += x; ny -= y; break;
case 1: nx += y; ny -= x; break;
case 2: nx -= y; ny -= x; break;
case 3: nx -= x; ny -= y; break;
case 4: nx -= x; ny += y; break;
case 5: nx -= y; ny += x; break;
case 6: nx += y; ny += x; break;
case 7: nx += x; ny += y; break;
}
return _blocksLight((int)nx, (int)ny);
}
void SetVisible(uint x, uint y, uint octant, LevelPoint origin)
{
uint nx = (uint)origin.X, ny = (uint)origin.Y;
switch(octant)
{
case 0: nx += x; ny -= y; break;
case 1: nx += y; ny -= x; break;
case 2: nx -= y; ny -= x; break;
case 3: nx -= x; ny -= y; break;
case 4: nx -= x; ny += y; break;
case 5: nx -= y; ny += x; break;
case 6: nx += y; ny += x; break;
case 7: nx += x; ny += y; break;
}
_setVisible((int)nx, (int)ny);
}
readonly Func<int, int, bool> _blocksLight;
readonly Func<int, int, int> GetDistance;
readonly Action<int, int> _setVisible;
}
Further Possibilities
Here are some ideas for additional lighting possibilities that can be implemented on top of any of the above FOV algorithms.
NetHack-style lighting
In NetHack, the player has an unlimited sight radius, but outside of a certain minimum distance the player can only see tiles if they're "lit". An example is below. The player is in a dark room but can see the adjacent tiles due to the player's minimum sight radius of 1. The player can also see some tiles from the room down the hall because they're lit and unoccluded.
┌──────┐ ┌─────┐ │∙∙∙∙∙∙│ ┌───┐ │∙∙∙∙∙│ │∙∙∙∙∙∙│ │∙∙∙│ │∙∙∙∙∙│ │∙∙@∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙■∙∙∙∙∙│ │∙∙∙∙∙∙│ │∙∙∙│ │∙∙∙∙∙│ │∙∙∙∙∙∙│ └───┘ │∙∙∙∙∙│ └──────┘ └─────┘
┌──────┐ ┌─────┐ │∙∙∙∙∙∙│ ┌───┐ │∙∙∙∙∙│ │∙∙∙∙∙∙│ │@∙∙│ │∙∙∙∙∙│ │∙∙∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙■∙∙∙∙∙│ │∙∙∙∙∙∙│ │∙∙∙│ │∙∙∙∙∙│ │∙∙∙∙∙∙│ └───┘ │∙∙∙∙∙│ └──────┘ └─────┘
┌──────┐ ┌─────┐ │∙∙∙∙∙∙│ ┌───┐ │∙∙∙∙∙│ │∙∙∙∙∙∙│ │∙∙∙│ │∙∙∙∙∙│ │∙∙∙∙∙∙■∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙■∙∙∙∙∙│ │∙∙∙∙∙∙│ │∙∙∙│ │∙∙∙∙∙│ │∙∙∙∙∙∙│ └───┘ │@∙∙∙∙│ └──────┘ └─────┘
As you can see, lit tiles aren't light sources, so they don't illuminate other tiles. Instead, a lit tile is a tile that's been illuminated by some light source. With one possible exception (described below), only a small change to a field-of-view algorithm is needed to obtain NetHack-style lighting. First, have both a minimum and maximum sight radius and a way to tell if a tile is lit. The minimum radius is the radius of the player's carried light source (or "miner's hat"), and the maximum is how far the player can see even under perfect conditions. (The maximum may be infinite, since most roguelike maps tend to be fairly small compared to the limits of humanoid vision.) Whether a tile is lit is usually decided during dungeon generation. Second, run the algorithm out to the maximum light radius and set a tile to be visible if it would normally be visible and either it's within the minimum light radius or it's lit.
There's one consideration that isn't addressed by the above. If a floor tile is lit, then it doesn't matter which direction it's viewed from, but if a lit tile is a wall, then it does matter. For instance, if a room is lit then it only makes sense for the wall tiles to appear lit if you can see the side facing into the room. If you dig a tunnel to the back side of the wall, it should not appear lit because light from the room cannot reach the other side. There are several ways this can be dealt with:
- Don't allow it. If the player cannot dig through walls in your game, then you simply need to avoid generating walls that are supposed to be lit on one side but not another.
- Don't show lit walls as lit unless the player is in the room. This avoids the problem without restricting the player but prevents the player from looking down a hallway into a lit room and seeing the back wall lit. This still provides the main benefit of lit tiles, which is to let the player know about items, monsters, and rooms from a distance, but it could be considered a visual artifact.
- Use a simple heuristic. A wall tile is considered lit by the FOV algorithm only if the previous tile was considered lit. This has the effect that the FOV algorithm must pass over a lit floor tile before a wall behind it can be illuminated. (This consideration includes the floor tile the player is standing on.) I think this would work in every reasonable case, but perhaps your game is unreasonable.
- Instead of just having wall tiles, have four different types of wall tiles, indicating the direction the wall is facing, with the assumption that a lit wall tile is lit from the direction it's facing. (Alternately, have a bitmask, allowing a single wall tile to face multiple directions.) Then, a wall is only considered lit by the FOV algorithm if it encounters the wall from the correct direction. This enables the additional feature that walls might not look like walls unless the player sees them from the correct side, so if the player digs a tunnel to the back of a wall, it will not appear like a wall unless the player has already seen it from the other side.
- Instead of just tracking whether a wall tile is lit, track the direction from which it's lit or have four lit flags, one for each direction. Then, the FOV algorithm only considers a wall tile lit if it encounters the wall from a lit direction. This is similar to the previous suggestion except that a wall tile will appear to be a wall regardless of which side it's seen from (unless you implement that some other way), and it works better if light sources can move or be created or destroyed.
While the above method works, it's not especially efficient. While this doesn't matter if only the player has decent vision, if monsters can see equally well and many monsters are being simulated on each turn, it would be preferable if we didn't have to run the FOV algorithm out to an infinite distance in all directions for all monsters. Some ideas for optimizing NetHack-style lighting follow.
- First, make use of the fact that in NetHack, all (or almost all) lit rooms are convex, and a key property of a convex region is that if you're within it you can see every part of it. So as a first step, you can check if the player is within a lit, convex room and if so set all tiles within the room to be visible. This takes care of the very common case in which the only visible lit tiles are in the same room as the player.
- With NetHack-style lighting, the minimum sight radius is usually 1 and all FOV algorithms work identically at a radius of 1, setting all adjacent tiles to be visible. Whenever the minimum sight radius is 1, you can special case it to simply set all adjacent tiles to be visible.
- With #1 done, we need only concern ourselves with lit tiles outside the player's current room (and whatever tiles
would be exposed by the minimum sight radius). The map should have a list of the lit areas and their bounding boxes.
At this point, you can take one of two approaches.
- Run the FOV algorithm once for the minimum sight radius. Then run it again for each lit area besides the one the player is currently in, initializing it so that it only scans in the direction of the lit area. If you have more than 5-15 lit areas, option b may be more efficient.
- If the minimum sight radius is 1, set each adjacent tile to be visible. Then have an array of eight integers that represent the maximum sight radius that the FOV algorithm will need to scan in each of the eight octants. Initialize each element with the minimum sight radius if it's greater than 1, or with zero otherwise (since a minimum sight radius of 1 was already handled). Step through each lit area besides the one the player is currently in, determine which octants it's in, and increase the distances in those octants to the distance to the furthest part of the lit room. Then run the FOV algorithm once for each octant, using the octant's computed maximum sight radius.
- A further optimization that can be applied to either approach in step #3 is to keep track of the exits of the convex area that the player is in. These can be the exits from a room or the tiles at the points where a corridor changes direction. If there is no overlap between the sector leading to the lit room and a sector leading to an open exit from the area the player is in, then there is no way for light to pass through an exit towards the lit room, so the lit room can be skipped. Alternately, you can maintain a bitmask for each tile that indicates which lit rooms are visible from that tile (assuming all doors are open), and then only consider those in step #3. Both of these additional optimizations may require some data to be recomputed if the map changes.
In the image above, the octants are in red, the light yellow tiles are lit (but not necessarily visible), the two pairs of green lines delimit the sectors from the player to the two lit rooms, and the pair of blue lines is the result of a FOV scan in the direction of the rightmost lit room. If the first approach in step #3 above is used, the sectors to each lit room would be scanned. In the second approach, the maximum distance for each octant would be determined (6 for octants 0 and 1, 9 for octant 3, and 0 for the other octants, assuming a Chebyshev distance metric) and a FOV algorithm would be run for the octants with nonzero distances. If either of the further optimizations in item #4 above was used, the leftmost lit room would not be considered, and only octants 0 and 1 would be scanned.
Light sources
You can also have light sources, which are objects that emit light and illuminate the tiles around them, such as torches and magic gems. If a light source is wielded by the player, you can simply increase the player's minimum sight radius to match the radius of the light source, but if the light source is wielded by another monster or placed on the map, you can use the strategy of NetHack-style lighting described above. The main difference is that in addition to (or instead of) fixed lit areas generated with the map you also have temporary lit areas generated by light sources. The lit areas need not be rectangular, although their bounding boxes should be known. To determine the tiles lit by a light source, you simply run the FOV algorithm from the position of the light source with a maximum radius equal to the radius of the light source. The tiles "visible" to the light source are the ones lit by it.
┌───────────────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙o∙∙∙∙∙│ │∙∙∙∙∙∙@∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙│ └───────────────────────┘
Light falloff
You may not want lit tiles, whether permanently lit or lit by a light source, to be visible from an infinite distance, since in a dark dungeon the light scattered from them would be attenuated over a distance. If all lit tiles have the same brightness and thus the same distance that they can transmit light, then this can be implemented by simply making the maximum sight radius used by the FOV algorithm (when finding distant lit tiles) no greater than the distance that a single tile can transmit its light. Alternately, if you have variable tile brightness, you can just check when finding a lit tile outside the player's sight radius whether the player is close enough to it, and when a light source illuminates a tile you can increase the tile's brightness based on the distance from the light source.
Colored lighting
If you have light sources then in addition to propagating light you can propagate the color of the light as well, and instead of simply marking tiles "lit", you can add the color of the light to the tile's color. The resolution of the color can be 1-16 bits per color channel, and the channels might be red, greed, blue, and possibly brightness. A brightness channel is useful if you're using 1-bit color channels, since the standard text display has 1 bit per color plus a brightness bit. With more bits per color channel you can infer brightness directly from the color intensities much as a grayscale image can be computed from a color image.When adding a light source's color to a tile, there are four options for combining colors, but I think one is clearly preferable:
- First, you can simply add and saturate. If bright yellow light is shone on a tile you may get the RGB color (255, 255, 0). If a bright red light is also shone onto the tile, the resulting color would still be (255, 255, 0), since the red channel has been saturated. This allows the color additions red + blue + green = white and medium yellow + medium red = bright orange, but not bright yellow + bright red = bright orange or medium yellow + medium red = medium orange. Saturation is not physically correct but it's simple and produces decent results in most cases.
- Second, you can blend the light color into the tile color. If a bright yellow light and a bright red light are shone on a tile, you get the RGB color (255, 127, 0) which is bright orange. This is nice, but other combinations are not so nice. For example, bright red + bright green is not bright yellow but medium yellow, and red + green + blue is a blueish color, not white or even gray. Blending is not physically correct and simply doesn't work well with more than two colors. I'd only recommend it if you'll only blend up to two colors and you really want to favor dim colors.
- The third option is to use high dynamic range and rescale based on the most intense color. For instance, you might use colors with 8 bits per channel in your game. You can then have 8-bits per channel in your light sources and 16-bits per channel in your tiles. Then, to take the same example, a bright yellow and bright red light shining onto a tile would add together to produce the RGB color (510, 255, 0). Then, to obtain the actual color you take the most intense channel (red: 510) and compare it to the maximum value allowed in the color channel (255). Since it's greater, you rescale the color by a factor of 255/510 = 50%, resulting in the RGB color (255, 127, 0), which is bright orange. (If the most intense channel is not out of range, don't rescale.) Bright red + bright yellow = bright orange and red + green + blue = white, although medium yellow + medium red = bright orange, which is physically correct but may not be what you want. This is the best option in general because it's the most physically correct.
- The fourth option is to use high dynamic range and average the colors. This works much like a combination of the previous two options, and is really just a form of color blending that works with more than two colors (although even for two colors or less it's an improvement over basic color blending). You'll need to keep track of how many lights have been added together. Adding bright red and bright yellow produces RGB (510, 255, 0) and since two lights were added the result is divided by 2 to obtain to output color, yielding RGB (255, 127, 0). This allows bright red + bright yellow = bright orange and medium red + medium yellow = medium orange, but red + blue + green = gray rather than white. I'd only recommend this method if you want dim colors to add together into dim colors.
┌─────────────┐ │∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙│ │∙∙∙∙∙∙∙∙∙∙∙∙∙│ └─────────────┘
with 1-bit color channels
Colored lights can allow for nice atmospheric effects when near lava or mana pools, or if your game has animated spell effects (in which case a wand of lightning or fire could generate colored light). However, the question arises as to whether lights should color monsters and items on the ground as well, or just floor and wall tiles. Physically speaking, any object illuminated solely by a red light must appear red or black, so that is an argument for coloring monsters and items. But I'm of the opinion that monster and item colors displayed in traditional roguelikes do not represent the actual colors of objects but rather the types of objects. A giant bee should still appear yellow even if the player's creature is seeing it with darkvision or infravision or under a red light, since the player's creature can identify the bee by its shape and the color yellow communicates to the player that his creature sees a bee. That said, if your roguelike uses graphics tiles that allow the player to recognize things by shape, then it might in fact be a nice effect to tint them by the color of the light illuminating the tile. A similar argument can be had about special floor tiles, such as tiles of ice. It may be worth displaying them as white or bright cyan rather than coloring them based on the light because colored ice is still recognizable as ice and that's worth communicating to the player.
Comments
Still, useful. But it'll take some time to digest it all.
Eg:
>case 0: return GetAllowFlow(x1 + x2, y1 - y2);
Since I believe this method is called in a tight loop, assigning the nx/ny variables is a little wasteful. I also tried to use ref/out in my delegates for the construction, but this required a custom delegate type and did not support lambda expressions, making it harder to use, but if you can change these function calls so that they pass, rather than copy variables, again you should see a significant boost.
The tile is divided up to allow all the corners of the tile geometry - beveled and unbeveled walls, and the inner square - to be referenced, since it's the corners that mark the boundaries where light begins to intersect the geometry.
Regarding the first potential optimization you mentioned, you may or may not be right but such things should be tested because the results are often unexpected. With a smart compiler it'd be the same either way, but I don't know if the .NET JIT compiler is smart enough. I recommend trying it out and seeing if there's a significant improvement. My suspicion is that it would be minor at best, but I haven't tried it myself.
Regarding the delegates passed to the constructor, you can use ref/out parameters with lambda expressions using the 'delegate' keyword (Func(1, 2, delegate(out int x) { x=5; });) or by specifying the type (Func(1, 2, (out int x) => { x=5; })). I don't think you'll see a performance improvement from that, though. The parameters are simple integers. In general, it's slower to use integers by reference. Even replacing two integers with a reference to a single Point structure is likely slower. (Obviously it depends on what the functions do, but I expect that using references would not be faster in any realistic function.)
Anyway I don't actually expect people to use delegates. I used them to remove extraneous information (such as the map representation and game logic) from the article so I could focus on the vision algorithms. You can just replace them with normal function calls and make the vision calculator a static class or singleton if that's suitable for your project. In my own project, the vision calculator is not even a class, but just a function.
The only omission I found was, you never actually say what language your code is in (as far as I can tell). It looks like C#, and you did mention .NET in nthe comments above, so I suspect that's what it is. But it'd be nice to be explicit.
Anyway, I'm going to try this out for an educational roguelike for iOS that my boys and I are working on. Thanks for the leg up!
However, I also have to balance my appreciation for flood-fill style FOV (some call it diamond FOV? http://www.oocities.org/temerra/los_rays.html). Diamond FOV has the nice property of diagonal spaces acting as connected diagonal walls, which is a modification I'd like to make to your algorithm as it is appropriate to my game.
Do you have any advice how you would modify your algorithm to account for diagonal spaces becoming connected diagonal walls that block light?
If I understand you correctly, you want a string of tiles connected diagonally to act as a solid wall. Would characters be able to move diagonally along the wall? It seems like they should be able to, but then that introduces ambiguous cases where it's not clear how to turn a group of blocks into diagonal walls. (It's easy to draw such a case on a piece of paper, but I don't have time to do it on the computer.) Anyway, if you make sure to avoid ambiguous tile arrangements when generating the map, or treat them as impassible, then I think it's doable.
I don't have time to write any code write now, since it's the holiday and I'm about to go out, but I'll try to think about it relatively soon.
I finally got time to work on this. Since you didn't give me your email address, I just put the code into this pastebin link: http://pastebin.com/2nTK50sg It's something of a hack because I didn't try to fit the modifications in to the rest of the code and optimize them, but it should work.
Good luck!
I do appreciate the simplicity in comparing the two variants. Besides, I can live with a handful of extra BlocksLight calls. It's okay since the algorithm is still the most robust vision algorithm I know of!
Thanks again!
I have a question about the code in Shadow casting.
Shouldn't GetDistance(x, y) in
bool inRange = rangeLimit < 0 || GetDistance(x, y) <= rangeLimit;
be GetDistance(tx, ty) instead? since x is always between 1 and rangeLimit regardless of the origin position.
By the way, what is LevelPoint? Is it a struct for storing x/y coordinates of a map?
https://github.com/jeanmerlet/ruby_games/blob/master/dungeon/systems/fov.rb
The code looks extremely different, but I am fairly convinced it's the same based on testing. At least diagonal spaces, blind corners, and narrow passages are identical. However, I am not 100% that expansive walls are the same, though I am not using a symmetrical version of the algorithm. Can rectangular rooms theoretically still have unlit corners with a correct implementation of the asymmetrical version of your algorithm?
Anyway, thought you might like to know :>
I tried a few quick hacks to work around this, but it is more complicated than it might appear. I suppose I can just claim it is a feature instead of a bug.
That said, real vision doesn't have a radius where there's a sharp line between what's visible and not. Rather, things get dimmer, blurrier, more confusing, and more open to misinterpretation as they get harder to see. You could easily justify showing some tiles just outside the FoV radius by saying that they're barely visible but are easy for the character to interpret (e.g. corners in an apparently rectangular room), compared to other tiles that are also barely visible but are too hard to interpret (e.g. a box-like shape on the floor that could be many things).
So you can argue either way, but I'd say it's not a bug given that it fits how roguelike vision algorithms traditionally worked.
Apart from that, I will have to draw things out and take some time to really understand what's going on. It's not trivial.
The comments state that this function should return the distance from the origin (0, 0). My question would be: why do you need this function at all then? If the origin is always (0, 0), then the distance calculation should always be same right and could be part of the class? Perhaps something like sqrt(x^2 + y^2)
Or is this an error in the comment and is the origin assumed to be the origin of the light and it can be any other point than (0,0)?
My current implementation of lighting uses a bitmap to record which tiles are light. I run the vision algorithm for each light source to update the lit bitmap. The player is also a light source (miner's hat). I run the vision algorithm on the player and all tiles that are "lit" and within the FOV are "visible". Visible tiles appear bright. Invisible tiles (that were previously visible) appear dark. Unexplored tiles appear black. That's my interpretation of Nethack-style lighting.
It has the same problem that you described. Walls appear visible from outside of the room. I'm not really sure how to solve it. I tried to "Use a simple heuristic" and it didn't work (either because the algorithm doesn't process tiles in the right order or I'm implementing it incorrectly). Tracking the direction that a wall tile is lit seems like the ideal solution but how do I know which direction the wall was lit from? I don't think I can check the octant and I certainly can't just compare the position of the wall to the position of the light. I need to do something "smart" and I can't figure it out.
Another question I had was the use of unsigned integers. Is there any particular reason for using them? Will I encounter any subtle bugs if I replace them all with signed ints?
Unsigned integers are used because they're slightly more efficient in some operations. I don't think using signed ints will cause any problem, assuming you do the conversion correctly. It will reduce the maximum map size by half, but that won't matter unless your maps are hundreds of millions of tiles wide.
As for your other question, I think the question of which side a wall is lit on is closely related to the direction of the wall. Some walls are north-south, others are east-west, others are intersections or corners, etc. You can figure out this shape of the wall by seeing what the other wall or door tiles are in the four cardinal directions around it. If there are walls or doors above and below but not to the sides, then it's north-south, etc. Now, maybe your game doesn't display walls in the traditional way, but nonetheless it remains true that by examining the surrounding four tiles you can tell the direction of a wall or door. This information doesn't change (unless wall or door tiles are created or destroyed), so it can be computed only once (or when the map changes).
Then, knowing the direction of a wall, you can just compare the position of the wall to the position of the light. A north-south wall can only be lit from the east or from the west. An east-west wall can only be lit from the north or from the south. A light lights a corner or intersection from either two directions (if the light strikes an acute or "inside" angle) or a single direction (if it strikes an obtuse or "outside" angle). The set of directions a wall or closed door is lit from can be efficiently stored in half of a byte, using one bit per lit direction.
The reason the direction of the wall dominates the answer is because, unlike a mirror, the wall is assumed to evenly diffuse the light incident upon it. As light strikes a wall from different angles, it doesn't reflect off at significantly different angles, it just reflects more brightly or dimly.
Finally, once you know the directions a wall or door tile is lit from, you can simply compare the position of the wall to the position of the player to see whether the player sees a lit side. Now, the directions a wall is visible from depend on the wall shape in exactly the same way that the directions a wall is lit from do - again for the reason that light is assumed to diffuse from the wall evenly. So a north-south wall can be seen from the east or west, etc. It's the exact same calculation (so you can use the same function), and it gives you a bit mask of directions the player could see the wall from, if it was lit. Then you simply bitwise AND that mask with the lit direction mask stored along with the wall tile, and if the result is nonzero the player can see the wall from that direction.
This gives me an idea for a simple way to compute those bitmasks, too. The direction of a wall can be represented as a bitmask describing which "faces" it has. A simple comparison of the X and Y coordinates of the light and tile can tell whether the light is coming from the north, south, east, and/or west, and these can be similarly stored in a bitmask. Then the two masks are simply bitwise ANDed together to produce the set of existing faces struck by the light.
I had an interesting challenge of implementing a vision algorithm for a homebrew Atari 2600 game. Needless to say, both RAM and CPU time are extremely limited, so most of the methods are not practical on the platform. I first implemented a ray casting algorithm using pre-computed lines, but I wasn't happy with the results.
My current method is to cast rays in 8 directions (orthogonal and perfect diagonals). For each of the remaining tiles, I look at two adjacent tiles that are closest to the player's tile, and if *either* of these tiles is visible and not solid; otherwise the tile is blanked out. Obviously the order tiles are checked matters since the two "parent" tiles to be checked need to have known visibility.
On the Atari, I pre-compute which tiles are the two adjacent tiles that are closest to the player to save precious CPU time, but probably on most other platforms this could be done fairly trivially on the fly.
The end result seems to be similar to the Permissive FOV, but with much less computation. I was wondering if you have heard of an existing algorithm that uses a similar approach?
I don't know how many CPU cycles you have to play with, but if I had to implement a minimally expensive vision algorithm I'd probably try limiting the sight distance (e.g. to 4) and using an algorithm hardcoded for the particular shape of the vision radius. That might be similar to what you meant by "pre-computed lines", but I don't know.
You could even use a look-up table if the sight radius was small enough! It'd have to be pretty small, though. A square sight radius of N could use a lookup table with (N+1)*(N+1)-1 bit inputs and outputs, so a sight radius of 2 would require 8-bit keys (i.e. 256 entries) with each entry being one byte. But such a small sight radius could be rather limiting.
For an arbitrary sight radius, shadow casting is the fastest good-looking algorithm I've seen on a modern CPU - not that I'm an expert on what new algorithms might exist these days - but the 2600 doesn't have a multiply instruction. Ray casting can be done without multiplication and might be better.
I'm curious about your algorithm, though. If you have some accurate pseudocode, feel free to share it. (I don't know what you're programming that homebrew game in; if it's 6507 assembly code I could probably read it since I used to program the 6502 25 years ago, but I'd prefer not to try digging up those memories. :-)
https://github.com/sarkahn/rltk_unity_roguelike/issues/2
This is obviously 100% a mistake I made in my implementation, if possible any hints on where I might have messed it up would be appreciated though!
I want to implement your Shadow Casting algorithm and I am trying to figure out a way to make it work with angles to check only within a defined "view cone" not a circle. Any idea if this is even possible using SC or how it could be achieved?
Slightly more complex would be a 90-degree vision cone, since you'd want to scan one full octant and two half octants, but it's still not that hard. You just change the initialization of the slopes for the octants on the edges. Instead of using 0/1 and 1/1, for example, you might use 0/1 and 1/2 to get a 22.5-degree slice rather than a 45-degree slice.
However, my use of it for lighting poses one problem which I don't think has been covered in the article or discussions, and that is that (I believe) this algorithm visits tiles on the octant borders twice. That isn't a problem when the "SetVisible" function sets some kind of data (visible=true), but e.g. when doing lighting you want to update data, like adding one light's contribution to the tile's total lighting data. Thus tiles along octant boundaries appear brighter than others.
Can you think of an elegant way of ensuring that tiles are visited once and only once? I used to have a solution where even octants wouldn't touch diagonals and odd octants wouldn't update non-diagonals. But that doesn't work well when you use this algorithm for view cones, where you don't run on all octants. I suppose there's always the good old "previously-visited set" solution but I'm not a fan of that if it can be avoided.
I've been considering the different interpretations of when a tile is visible, and I'm not sure if on/off is really the best way to go. If we're talking about a wall, or something that's too large to squeeze between 2 diagonal NetHack boulders, that should definitely be visible; ditto the floor terrain. If essentially all of the tile is visible (too little room not visible to fit the smallest scale monster). In-between, it really should be able to depend on how sneaky (and small) the thing in the tile is, versus the perception and time spent of the observer. (For something like a chest, the inner square you use should work well.) Your thoughts?
Variable brightness / distance from observer: I addressed this somewhat in the "light falloff" section, but you might want to go further and track the amount of light falling on a tile and attenuate it over the distance to the observer. A tile that's barely lit would be hard to see, as would a tile viewed from a long distance.
Sneakiness / size of objects: I think this could be implemented by scaling the effective distance to the object. A medium-sized object would have a scale factor near 1.0, so it gets harder to see over distance at the normal rate. A small object would have a scale factor less than 1, so it gets harder to see faster, and a large object may have a scale factor greater than one, so it's easy to see even at a distance.
Perception: This could be another scaling factor (e.g. a more perceptive character can see things further away), or it could be a random factor (e.g. a character has a random chance to see something based on its perceptiveness). However, once an object is perceived, it should stay observed perhaps even if it moves. This could be a hardcoded effect, or simply a bonus to perceiving the same object again. The bonus would be lost if the character failed a subsequent perception check.
There are various ways to combine all these factors. One simple way is to just multiply them all together and compare them to a threshold or use the value as a percentage chance of observing the object. Some factors may be combined linearly. Others might be nonlinear. Light, sound, and size all diminish nonlinearly, for example. You'd probably want it to be really hard to be sneak right next to somebody.
Facing: This isn't really related to vision per se, but I've experimented with characters having a field of view rather than being able to see 360 degrees around them. This allows stealth and sneakiness by remaining behind monsters or in their peripheral vision. Since most of the algorithms on this page work in octants, central and peripheral vision can be easily simulated by running the algorithm in the central octant(s) of the field of view with a higher perceptiveness factor than the octants on the edge of the field of view.
Other senses: I've also experimented with tracking by sound and scent. In my last unfinished roguelikes, there were 8 or 16 different scents and each type of creature could emit particular scent pattern. Scents were propagated slowly through the dungeon, blocked by walls, and mostly blocked by doors. Similarly, sounds were propagated instantly, mostly block by walls, and partly blocked by doors. These can all factor into a stealth / perception model.
Enemies can go through mental states like idle -> surprised -> alerted -> attacking. These transitions can individually be very fast "actions", i.e. less than a full turn, but the whole chain of transitions may still add up to a turn or two.
I am currently experimenting with the code, and I am trying to make it so that the "wall penetration" value is set as 0. I thought parameter x is what it is supposed to do since if I increase it the light penetrate the solid wall more.
However, I could not make it to be 0, so there is always one tile visible other than the origin itself.
So
x = 0 => min of 3x3 tile lit.
x = 1 => min of 5x5 tile lit.
How can we make it so that min lit block is 1x1 if the origin is surrounded completed by "opaque (blocked) tile?
x x x
x 0 x
x x x
If so I want only 0 to be visible where x is a opaque wall.
if(radius == 0) SetVisible(playerX, playerY);
else RunVisionAlgorithm(...);
Or, perhaps you don't want light to illuminate walls. In that case, I think there are two simple approaches: 1) Change the lighting code to not illuminate walls, i.e. change "if(isVisible) SetVisible..." to "if(isVisible & !isOpaque) SetVisible...". Or, 2) Change your rendering algorithm to simply not show walls.
Which brings me to my main question!
I notice that no algorithm performed the 100x100 empty map very quickly. I suppose that with a large enough sight radius, you have to write 10,000 values one way or the other. I was trying to come up with a good way to optimize this, such as maintaining rays or a polygon, but this obviously got quite cumbersome and not optimal for a small sight radius. You could probably limit the output to things that are actually rendered to the player or reduce the radius, but this might not be feasible if the project was a god game/simulation like Dwarf Fortress, for example.
It would be handy to have light sources and vision handled by similar code. One thing I want to avoid is arbitrarily limiting data because of hardware constraints, eg a hard limit of 16 or 32 radius vision. Always curious to see how people optimize things
I'm sure you can optimize the algorithm for at empty or nearly empty map, in the max vision range case. If the whole map is visible there's no need for any fancy vision algorithm! The "Outdoor (100x100)" test, which simply added random one-tile pillars on 25% of the space, was much faster, at 140925 times per second even with an unlimited sight radius. (That's faster than the empty map with an 8-tile sight radius.) So having even a few obstacles to block sight helps a lot.
I think the most important thing is to not invoke the full vision algorithm unnecessarily. For instance, if a character hasn't moved and the dungeon hasn't changed (e.g. doors opened or closed), then you can simply use the same visible area as before. (Even if the dungeon does change, it won't affect the visible area if the changed tiles are outside the visible area.)
It's also important to have a fast way to compute the BlocksLight call. Optimization within the map representation, so BlocksLight is a simple comparison and not looking at multiple tiles, helps with that.
Another thing you can do is trade space for time. A cache of bitmaps of visible tiles can be stored from each position, such that returning to a position whose sight map is already known means you can just reuse the existing sight map. This is an extension of the "don't recompute the sight map if it hasn't changed" idea, except that now you remember multiple sight maps.
But as always, it's important to profile and find out where time is really being spent. In my own games, the vision algorithm wasn't the biggest part, even though every monster ran the full vision algorithm (not just the player). Pathfinding, AI, sound propagation, and other bits may be more expensive...
i love this comparison and especially your algorithm and i would like to implement it myself but i have one issue.
When calling the recursive compute function you supply it with a bottom struct initialized with x: 0 and y: 1.
But later down you have this line:
bottomY = ((x*2-1) * bottom.Y + bottom.X) / (bottom.X*2);
In my implementation i get a can not divide by zero, because bottom.X is zero
As far as i can see there is no way for the algorithm to change the value of bottom.x before this happens so this exception should happen regradless of input parameters?
Do i understand something wrong here?
so... i am stupid :D
i messed up the x / y order on some functions.
What confused me is that x is not always the first function argument.
So anyway, it is fixed now and working great!
Thank you again for the algorithm and this great writeup!
greetings, Gebäck
the problem is with beveled edges, I don't know how the algorithm works so I don't know if the beveled edges feature is implemented or not (I just copied it) and I noticed some weird issues, mainly when standing outside a door, I only see when block infront of it (among other things) help please?
I sent it by mail
One question (not sure I just missed the explanation in your post)...
In section Comparison, subsection Pillars, where player @ is centered at the left side and the vertical wall at the right side is lit, but asymmetrically lit; at the upper end the top tile is lit but at the low end it's unlit.
We see this asymmetry in the output of all algorithms presented. I'm not sure about the source of that (maybe an inappropriate or asymmetric definition of an "octant", or a 'lt' vs. 'le' quasi off-by-one issue, or something else?). It appears to me to be an unnecessary effect or artifact. Or is it deliberately designed that way (e.g. for performance reasons or to avoid other effects)? - Could you provide a hint, please?
See the section of the page where I wrote "In this and subsequent sections I've reduced the line height of some sections in order to make the height of a tile closer to its width, allowing a better sense of symmetry on the two axes. Depending on your font and browser, this might look terrible, especially in vertical walls. To toggle this effect, click here."
Try clicking that link to toggle the effect and see if it resolves it for you.
bool inRange = rangeLimit < 0 || GetDistance(tx, ty) <= rangeLimit;
tx and ty should be replaced with x and y:
bool inRange = rangeLimit < 0 || GetDistance(x, y) <= rangeLimit;
It might be my implementation that's screwed up or something that only happens in Rust but I'm not sure. I'd rather not see (9,14) and (11,14) at all from (10,10).
#.#
...
.@.
If I stand in top left I cannot see the @ but I can see the top left from @.
...
#.#
...
...
.@.
Standing at the bottom I got these results (where 1 is visible and 0 is not):
010
111
111
111
1@1
From the top-left corner I got these results:
111
@11
011
001
001
So, for that pair of tiles, it seems to work, in that neither tile is visible from the other. I also ran an exhaustive search over that map, trying every pair of points and got similarly successful results. I suspect there is a mistake in your translation to Rust...
@11
111
011
001
001
Thanks for your help!
https://gist.github.com/xErik/ace707bc9047809f5991e4b4d58d9fb2
The port sticks to the original except that:
(a) It provides a symmetry switch.
(b) It returns all coordinates inside the circle plus individual visibility indicators.
I took great care to make the code mirror your code.
Could it be that the recursive call of "compute()" is responsible for that?
LinkedListNode<Field> steeper = currentField, shallower = activeFields.AddBefore(currentField, currentField.Value);
What is actually being assigned to the LinkedListNode "shallower"? Looking up the C# method, LinkedList.AddBefore doesn't seem to return any value (void) ?
source: https://learn.microsoft.com/en-us/dotnet/api/system.collections.generic.linkedlist-1.addbefore?view=net-7.0
God bless.
I have a question though, I have added this to my game and everything is working as it should, sweet. But, I am having issues with cells being permantly visible, since nowhere in script is the visibility returned back to false. I kind of thought that the light falloff section was adressing this, but couldn't grasp what that meant.
How should I go addressing this, again hiding cells that go out of visibility, do you have any tips? At the moment I am setting everything back to not visible once cells are drawn once, but that leads to issues in cell-selection (you should only select visible cells).
Again, thank you for your work!
Regards, Alex
I know that you can check that a monster can see the player by checking whether the player can see a monster. But if I want to check if a monster can see another monster, but won't be using an entire visibility map for either monster, then an LoS algorithm that perfectly matches this algorithm's results would be what I need.
Thanks for this awesome algo!
The algorithm normally scans eight octants, and for each octant it initializes the top line slope to 1 and the bottom line slope to 0, representing the octant's 45-degree slice. If the target monster is instead at (10,4) relative to the viewer (after rotation into the octant), you could initialize the top line to touch the top-left corner of its inner square, and the bottom line to touch the bottom-right corner of its inner square. Since the formulae for the top-left and bottom-right corners are (y*4+1) / (x*4-1) and (y*4-1) / (x*4+1) respectively, you'd initialize the top line to 17/39 and the bottom line to 15/41. Also, set the maximum sight distance to the distance to the target. Then run the algorithm as normal. It would only scan a very narrow beam.
Now, the only wrinkle is when the monster happens to be on the border between two octants. In that case, you'd have to try it for one of the octants, and if it's not visible there, then try it again for the other octant. In one case, you'd set the top line to 1/1 (rather than allowing it to exceed 45 degrees) and in the other case you'd set the bottom line to 0/1 (rather than allowing it to become negative).
That's the easiest approach, I think. It may be possible to make use of the knowledge that the beam is very narrow to optimize the inner loop, but it's probably not worth the effort. Also, there's no need to update a visibility map; you only need to report a boolean value at the end, telling whether or not it reached the maximum sight distance.