Web Rarely

One night while in bed I was struck by an idea for a more efficient flood-fill algorithm, and unlike many of my bed-based ideas this one still worked in the morning. It's optimized for speed and a shallow recursion depth, and it doesn't require any heap-based memory allocation. It will always fill a rectangle without any recursion, and can fill any convex shape and many concave shapes without recursion as well depending on the initial point. It is much faster than the scanline method (commonly considered state-of-the-art) in the case where testing whether a pixel should be filled is a fast operation and either somewhat slower or somewhat faster in the case where testing a pixel is a slow operation (depending on the particular scanline method implementation).

Behold the textbook four-way flood-fill algorithm:

function fill(array, x, y)
  if !array[x, y]
    array[x, y] = true
    if y > 0: fill(array, x, y-1)
    if x > 0: fill(array, x-1, y)
    if x < array.width-1: fill(array, x+1, y)
    if y < array.height-1: fill(array, x, y+1)

Or, in C# with bottom-level call elimination:

public static void BasicFill(bool[,] array, int x, int y)
{
  if(!array[y, x]) BasicFill(array, x, y, array.GetLength(1), array.GetLength(0));
}

static void BasicFill(bool[,] array, int x, int y, int width, int height)
{
  array[y, x] = true;
  if(y > 0 && !array[y-1, x]) BasicFill(array, x, y-1, width, height);
  if(x > 0 && !array[y, x-1]) BasicFill(array, x-1, y, width, height);
  if(x < width-1 && !array[y, x+1]) BasicFill(array, x+1, y, width, height);
  if(y < height-1 && !array[y+1, x]) BasicFill(array, x, y+1, width, height);
}

A lot of people use this algorithm, because it's simple and it works well enough for small regions. However, the algorithm will rapidly overflow the stack with larger regions. To avoid this, there are more sophisticated methods. The right-hand fill method uses a fixed amount of memory but is quite complicated and can be quite slow. The best of the popular methods is, I believe, the scanline method. It works by maintaining a stack of line segments that need to be filled. The scanline method is usually much faster than the basic fill method (depending on the variant and the shape being filled), and more importantly uses much less memory. Unfortunately, due to the order of cell access its memory needs to be allocated on the heap, which adds pressure to the garbage collector.

Implementations of the two common scanline variants are given below. The first is the standard variant, which performs nearly the minimum number of pixel tests and is optimized for the case where pixel testing is a slow operation, for instance when the pixel test must do color space conversion and compare pixels against a threshold of similarity. (This variant is a simplified and bug-fixed version of the Javascript code given here.)

public static void ScanlineFill(bool[,] array, int x, int y)
{
  if(test(array[y, x])) return;
  array[y, x] = true;

  int height = array.GetLength(0), width = array.GetLength(1);
  Stack<Segment> stack = new Stack<Segment>();
  stack.Push(new Segment(x, x+1, y, 0, true, true));
  do
  {
    Segment r = stack.Pop();
    int startX = r.StartX, endX = r.EndX;
    if(r.ScanLeft) // if we should extend the segment towards the left...
    {
      while(startX > 0 && !test(array[r.Y, startX-1])) array[r.Y, --startX] = true; // do so, and fill cells as we go
    }
    if(r.ScanRight)
    {
      while(endX < width && !test(array[r.Y, endX])) array[r.Y, endX++] = true;
    }
    // at this point, the segment from startX (inclusive) to endX (exclusive) is filled. compute the region to ignore
    r.StartX--; // since the segment is bounded on either side by filled cells or array edges, we can extend the size of
    r.EndX++;   // the region that we're going to ignore in the adjacent lines by one
    // scan above and below the segment and add any new segments we find
    if(r.Y > 0) AddLine(array, stack, startX, endX, r.Y-1, r.StartX, r.EndX, -1, r.Dir <= 0);
    if(r.Y < height-1) AddLine(array, stack, startX, endX, r.Y+1, r.StartX, r.EndX, 1, r.Dir >= 0);
  } while(stack.Count != 0);
}

struct Segment
{
  public Segment(int startX, int endX, int y, sbyte dir, bool scanLeft, bool scanRight)
  {
    StartX    = startX;
    EndX      = endX;
    Y         = y;
    Dir       = dir;
    ScanLeft  = scanLeft;
    ScanRight = scanRight;
  }
  public int StartX, EndX, Y;
  public sbyte Dir; // -1:above the previous segment, 1:below the previous segment, 0:no previous segment
  public bool ScanLeft, ScanRight;
}

static void AddLine(bool[,] array, Stack<Segment> stack, int startX, int endX, int y,
                    int ignoreStart, int ignoreEnd, sbyte dir, bool isNextInDir)
{
  int regionStart = -1, x;
  for(x=startX; x<endX; x++) // scan the width of the parent segment
  {
    if((isNextInDir || x < ignoreStart || x >= ignoreEnd) && !test(array[y, x])) // if we're outside the region we
    {                                                                            // should ignore and the cell is clear
      array[y, x] = true; // fill the cell
      if(regionStart < 0) regionStart = x; // and start a new segment if we haven't already
    }
    else if(regionStart >= 0) // otherwise, if we shouldn't fill this cell and we have a current segment...
    {
      stack.Push(new Segment(regionStart, x, y, dir, regionStart == startX, false)); // push the segment
      regionStart = -1; // and end it
    }
    if(!isNextInDir && x < ignoreEnd && x >= ignoreStart) x = ignoreEnd-1; // skip over the ignored region
  }
  if(regionStart >= 0) stack.Push(new Segment(regionStart, x, y, dir, regionStart == startX, true));
}

The second scanline variant is optimized for the case where pixel testing is a fast operation, for instance when doing a simple fill. It performs many more pixel tests but has lower overhead. I'll call this variant "Scanline FT". This implementation is not based on any published algorithm but is simply my own idea of how a flood fill that stores line segments might work. (I also came up with a version that did 1/3rd fewer pixel tests. In performance, it was between the two scanline variants given here.)

public static void ScanlineFTFill(bool[,] array, int x, int y)
{
  int height = array.GetLength(0), width = array.GetLength(1);
  // we'll maintain a stack of points representing horizontal line segments that need to be filled.
  // for each point, we'll fill left and right until we find the boundaries
  Stack<Point> points = new Stack<Point>();
  points.Push(new Point(x, y)); // add the initial point
  do
  {
    Point pt = points.Pop(); // pop a line segment from the stack
    // we'll keep track of the transitions between set and clear cells both above and below the line segment that
    // we're filling. on a transition from a filled cell to a clear cell, we'll push that point as a new segment
    bool setAbove = true, setBelow = true; // initially consider them set so that a clear cell is immediately pushed
    for(x=pt.X; x<width && !array[pt.Y, x]; x++) // scan to the right
    {
      array[pt.Y, x] = true;
      if(pt.Y > 0 && array[pt.Y-1, x] != setAbove) // if there's a transition in the cell above...
      {
        setAbove = !setAbove;
        if(!setAbove) points.Push(new Point(x, pt.Y-1)); // push the new point if it transitioned to clear
      }
      if(pt.Y < height-1 && array[pt.Y+1,x] != setBelow) // if there's a transition in the cell below...
      {
        setBelow = !setBelow;
        if(!setBelow) points.Push(new Point(x, pt.Y+1));
      }
    }

    if(pt.X > 0) // now we'll scan to the left, if there's anything to the left
    {
      // this time, we want to initialize the flags based on the actual cell values so that we don't add the line
      // segments twice. (e.g. if it's clear above, it needs to transition to set and then back to clear.)
      setAbove = pt.Y > 0 && array[pt.Y-1, pt.X];
      setBelow = pt.Y < height-1 && array[pt.Y+1, pt.X];
      for(x=pt.X-1; x >= 0 && !array[pt.Y, x]; x--) // scan to the left
      {
        array[pt.Y, x] = true;
        if(pt.Y > 0 && array[pt.Y-1, x] != setAbove) // if there's a transition in the cell above...
        {
          setAbove = !setAbove;
          if(!setAbove) points.Push(new Point(x, pt.Y-1)); // push the new point if it transitioned to clear
        }
        if(pt.Y < height-1 && array[pt.Y+1, x] != setBelow) // if there's a transition in the cell below...
        {
          setBelow = !setBelow;
          if(!setBelow) points.Push(new Point(x, pt.Y+1));
        }
      }
    }
  } while(points.Count != 0);
}

My own algorithm is based on the observation that if you're filling a rectangular area and you've filled the first row, then for the cells in subsequent rows you don't need to look upwards (because that would be in the previous row, which was already filled), or downwards (because that's the next row, which will be filled soon), or left (except at the beginning, because the previous cell in the row was just filled), or right (except at the end, because the next cell in the row is about to be filled). This allows us to fill entire rectangular blocks with relatively few pixel tests. Extending this logic a bit allows convex areas to be filled with few tests. The result is a method that's faster than the scanline method in many cases, uses about the same amount of memory, and doesn't need to allocate any memory on the heap.

An implementation of my flood-fill algorithm is below. Although it looks long, that's largely due to comments.

public static void MyFill(bool[,] array, int x, int y)
{
  if(!array[y, x]) _MyFill(array, x, y, array.GetLength(1), array.GetLength(0));
}

static void _MyFill(bool[,] array, int x, int y, int width, int height)
{
  // at this point, we know array[y,x] is clear, and we want to move as far as possible to the upper-left. moving
  // up is much more important than moving left, so we could try to make this smarter by sometimes moving to
  // the right if doing so would allow us to move further up, but it doesn't seem worth the complexity
  while(true)
  {
    int ox = x, oy = y;
    while(y != 0 && !array[y-1, x]) y--;
    while(x != 0 && !array[y, x-1]) x--;
    if(x == ox && y == oy) break;
  }
  MyFillCore(array, x, y, width, height);
}

static void MyFillCore(bool[,] array, int x, int y, int width, int height)
{
  // at this point, we know that array[y,x] is clear, and array[y-1,x] and array[y,x-1] are set.
  // we'll begin scanning down and to the right, attempting to fill an entire rectangular block
  int lastRowLength = 0; // the number of cells that were clear in the last row we scanned
  do
  {
    int rowLength = 0, sx = x; // keep track of how long this row is. sx is the starting x for the main scan below
    // now we want to handle a case like |***|, where we fill 3 cells in the first row and then after we move to
    // the second row we find the first  | **| cell is filled, ending our rectangular scan. rather than handling
    // this via the recursion below, we'll increase the starting value of 'x' and reduce the last row length to
    // match. then we'll continue trying to set the narrower rectangular block
    if(lastRowLength != 0 && array[y, x]) // if this is not the first row and the leftmost cell is filled...
    {
      do
      {
        if(--lastRowLength == 0) return; // shorten the row. if it's full, we're done
      } while(array[y, ++x]); // otherwise, update the starting point of the main scan to match
      sx = x;
    }
    // we also want to handle the opposite case, | **|, where we begin scanning a 2-wide rectangular block and
    // then find on the next row that it has     |***| gotten wider on the left. again, we could handle this
    // with recursion but we'd prefer to adjust x and lastRowLength instead
    else
    {
      for(; x != 0 && !array[y, x-1]; rowLength++, lastRowLength++)
      {
        array[y, --x] = true; // to avoid scanning the cells twice, we'll fill them and update rowLength here
        // if there's something above the new starting point, handle that recursively. this deals with cases
        // like |* **| when we begin filling from (2,0), move down to (2,1), and then move left to (0,1).
        // the  |****| main scan assumes the portion of the previous row from x to x+lastRowLength has already
        // been filled. adjusting x and lastRowLength breaks that assumption in this case, so we must fix it
        if(y != 0 && !array[y-1, x]) _MyFill(array, x, y-1, width, height); // use _Fill since there may be more up and left
      }
    }

    // now at this point we can begin to scan the current row in the rectangular block. the span of the previous
    // row from x (inclusive) to x+lastRowLength (exclusive) has already been filled, so we don't need to
    // check it. so scan across to the right in the current row
    for(; sx < width && !array[y, sx]; rowLength++, sx++) array[y, sx] = true;
    // now we've scanned this row. if the block is rectangular, then the previous row has already been scanned,
    // so we don't need to look upwards and we're going to scan the next row in the next iteration so we don't
    // need to look downwards. however, if the block is not rectangular, we may need to look upwards or rightwards
    // for some portion of the row. if this row was shorter than the last row, we may need to look rightwards near
    // the end, as in the case of |*****|, where the first row is 5 cells long and the second row is 3 cells long.
    // we must look to the right  |*** *| of the single cell at the end of the second row, i.e. at (4,1)
    if(rowLength < lastRowLength)
    {
      for(int end=x+lastRowLength; ++sx < end; ) // 'end' is the end of the previous row, so scan the current row to
      {                                          // there. any clear cells would have been connected to the previous
        if(!array[y, sx]) MyFillCore(array, sx, y, width, height); // row. the cells up and left must be set so use FillCore
      }
    }
    // alternately, if this row is longer than the previous row, as in the case |*** *| then we must look above
    // the end of the row, i.e at (4,0)                                         |*****|
    else if(rowLength > lastRowLength && y != 0) // if this row is longer and we're not already at the top...
    {
      for(int ux=x+lastRowLength; ++ux<sx; ) // sx is the end of the current row
      {
        if(!array[y-1, ux]) _MyFill(array, ux, y-1, width, height); // since there may be clear cells up and left, use _Fill
      }
    }
    lastRowLength = rowLength; // record the new row length
  } while(lastRowLength != 0 && ++y < height); // if we get to a full row or to the bottom, we're done
}

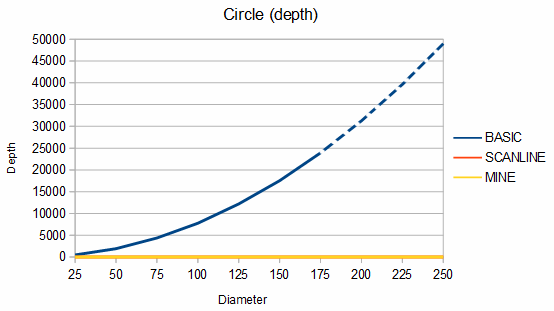
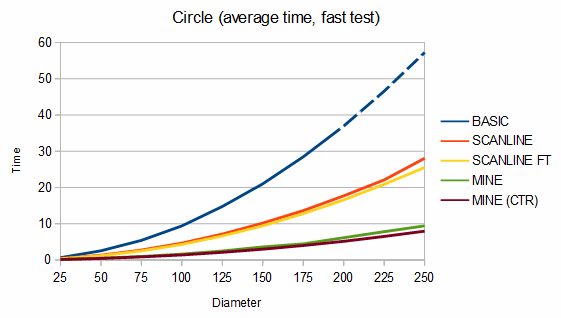
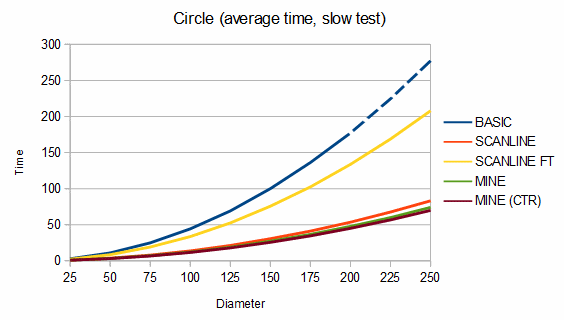
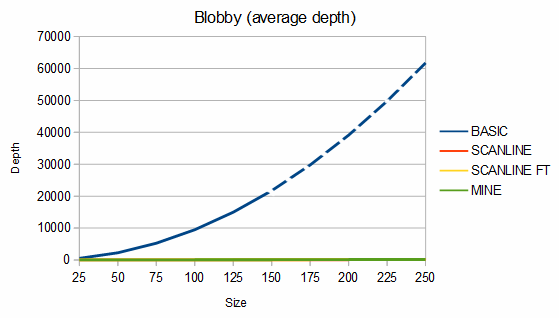
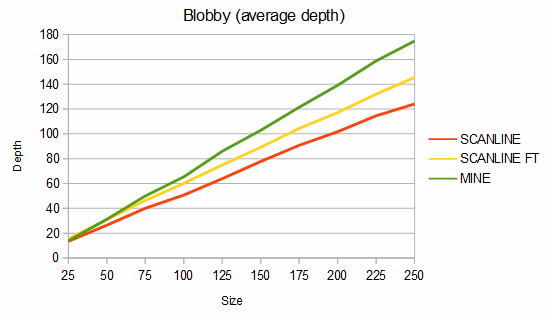
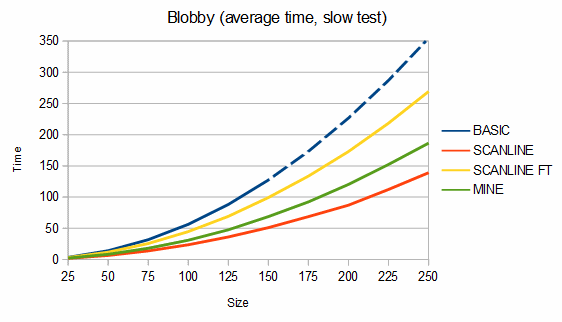
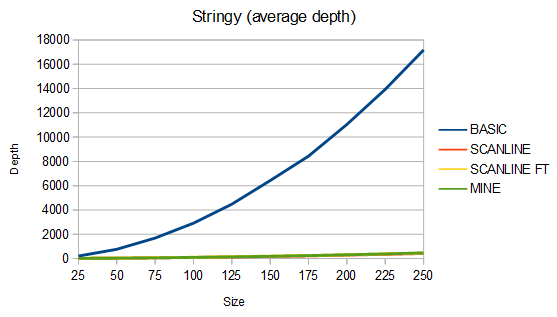
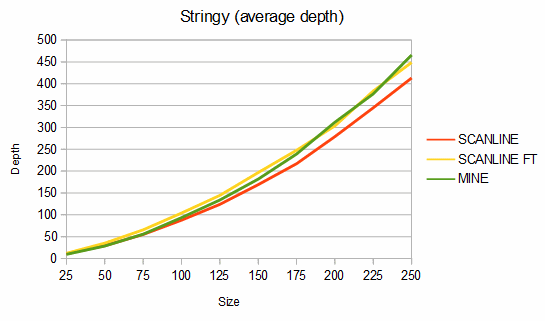
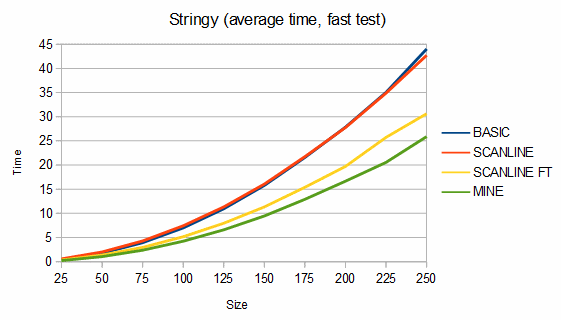
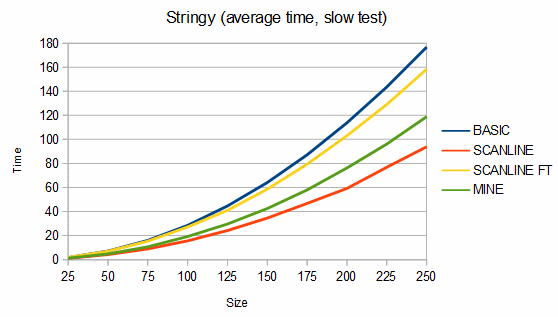
Below are some comparisons between the above algorithms for different shapes. The depth graphs show how much memory is required, based on either recursion depth or stack size. The time graphs show how much time is required. The "fast test" graphs refer to samples where pixel tests are fast and the "slow test" graphs refer to samples where pixel tests are slow. The dashed portions of the lines are extrapolations, which are needed because the basic fill method quickly overflows the stack. On all graphs, smaller numbers are better.

The first shape compared is a circle. The memory usage is almost identical between my algorithm (recursion depth = 0) and the scanline method (stack size = 2), but my algorithm is about 164-189% faster in the fast test case and about 12-190% faster in the slow test case. If the circle is filled using a point from where my algorithm can fill the entire circle as a single convex region (the MINE (CTR) line), it's about 6-16% faster still.

The second shape compared is a "blob", which is characterized by a mostly solid center and rough edges. An example blob is given below.

          **
          **
        *****
        ******
    *   *** * *
  * *   ***** *
  * *** **********
 ** * *********
  ************
** ********** *
***************
**************
* ***********
  ****** *
 ***** *****
  **** * * **
   ** **
      ****
     ** *

For blobs, my algorithm uses about 11-29% more memory than the scanline method but is about 40-84% faster in the fast test case and from 24% slower to 44% faster in the slow test case. For the charts, 100 different blobs of each size were used and the results were averaged.

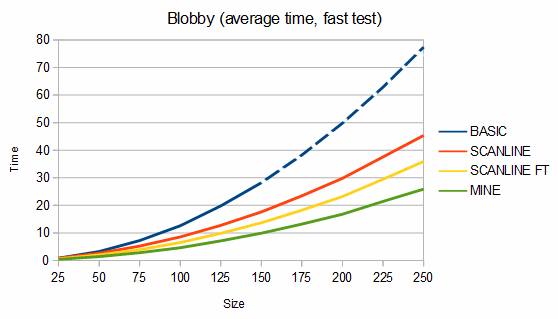
The third shape compared is "stringy", which is a shape characterized by thin connections between blobby parts. An example stringy shape is given below.

                   **
                   *******
                     ****
                      **
                    ****
                    *****
                     ****
                      **
                      ***
           *            **
         *****           ***
     *** ******          **
    ** ********          **
******  **** **          *
*********  ***        ** *
  *****     *     * *******
   ****     ********* *****
             *****      **
               ****
               *****
              *****
              ******
                ***

For stringy shapes, my algorithm uses from 8% less to 5% more memory than the scanline method, and is about 25-81% faster in the fast test case and from 17% slower to 40% faster in the slow test case. For the charts, 100 different stringy shapes of each size were used and the results were averaged.

Overall, I think my algorithm is a good general-purpose flood fill algorithm, and is faster than all scanline variants when pixel testing is fast. However, when pixel testing is slow, the standard (minimum-pixel-test) scanline variant usually performs better. My algorithm can also be sped up using pointers to eliminate repeated multiplication in the 2D array deferencing, but that requires "unsafe" code and anyway this is just an example of the idea.

All of the algorithms given here can be extended to 8-way flood-filling without too much effort.

NOTE: On December 3rd, 2017, I fixed a bug in my implementation after getting a report from a kindly reader. If you began using the code prior to then, see the change to the "if(lastRowLength != 0 && array[y, x])" block. The fixed version was exhaustively tested with all possible starting points in all possible 5x5 grids, so I'm fairly confident it's bug-free.